Авинаш Диксит - Стратегические игры

b) При каких значениях x в этой игре есть равновесие Нэша в смешанных стратегиях? С какой вероятностью, выраженной через x , каждый игрок будет выбирать стратегию «да» в равновесии в смешанных стратегиях?

c) Можно ли назвать эту игру при значениях x , найденных в пункте а, примером игры в доверие, игры в труса или игры наподобие тенниса? Обоснуйте свой ответ.

d) Пусть x = 3. Постройте график кривых наилучших ответов Ровены и Колина на координатной плоскости с осями p и q . Обозначьте все равновесия Нэша в чистых и смешанных стратегиях.

e) Пусть x = 1. Постройте график кривых наилучших ответов Ровены и Колина на координатной плоскости с осями p и q . Обозначьте все равновесия Нэша в чистых и смешанных стратегиях.

S9.Рассмотрите следующую игру:

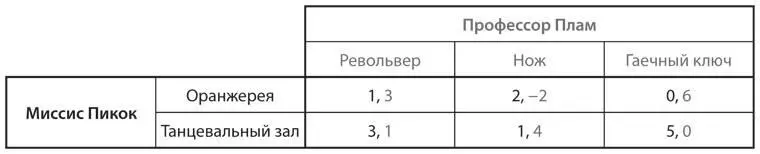
a) Постройте график ожидаемых выигрышей от каждой из стратегий профессора Плама как функции р -комбинации миссис Пикок.

b) При каком диапазоне значений p стратегия «револьвер» обеспечивает профессору Пламу более высокий ожидаемый выигрыш, чем стратегия «нож»?

c) При каком диапазоне значений p стратегия «револьвер» обеспечивает ему более высокий ожидаемый выигрыш, чем стратегия «гаечный ключ»?

d) Какие чистые стратегии профессор Плам использует в своей равновесной комбинации? Почему?

e) Найдите равновесие Нэша в смешанных стратегиях в этой игре.

S10.Многие из вас наверняка знакомы с детской игрой «камень, ножницы, бумага». В ней два игрока одновременно выбирают свой «камень», «ножницы» или «бумагу», складывая ладони так, чтобы их форма напоминала один из этих вариантов. Счет в игре ведется следующим образом. Игрок, выбравший «ножницы», побеждает игрока, выбравшего «бумагу» (потому что ножницы режут бумагу). Игрок, выбравший «бумагу», побеждает игрока, выбравшего «камень» (поскольку бумага обертывает камень). Игрок, выбравший «камень», побеждает игрока, выбравшего «ножницы» (потому что камень разбивает ножницы). Допустим, в каждом отдельном розыгрыше игры на кону стоят 10 очков. Возможные исходы игры представлены в следующей таблице выигрышей:

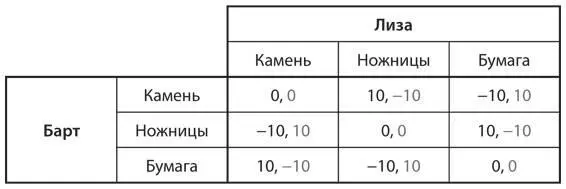
a) Найдите равновесие в смешанных стратегиях в этой игре.

b) Предположим, Лиза объявила, что применит комбинацию стратегий, в которой вероятность выбора стратегии «камень» составляет 40 %, «ножницы» — 30 % и «бумага» — 30 %. Определите наилучший ответ Барта на такой выбор стратегий. Объясните, почему ваш ответ резонный, основываясь на ваших знаниях о смешанных стратегиях.

S11.Вспомните игру между торговцами мороженым на пляже из упражнения U6в главе 6. В ней мы нашли два асимметричных равновесия в чистых стратегиях. В данной игре есть также симметричное равновесие в смешанных стратегиях.

a) Составьте таблицу этой игры пять на пять.

b) Исключите доминируемые стратегии и объясните, почему их не следует применять в равновесии.

c) Используйте ответ, полученный в части (b), чтобы найти равновесие в смешанных стратегиях в этой игре.

S12.Допустим, в игре в пенальти из раздела 7.Аданной главы в распоряжении бьющего игрока шесть стратегий: бить высоко и налево (ВЛ), низко и налево (НЛ), высоко и в центр (ВЦ), низко и в центр (НЦ), высоко и направо (ВП), а также низко и направо (НП). Вратарь по-прежнему располагает тремя стратегиями: двигаться налево от бьющего игрока (Л), двигаться направо (П) и оставаться в центре (Ц). Проценты успешных действий игроков приведены в следующей таблице:

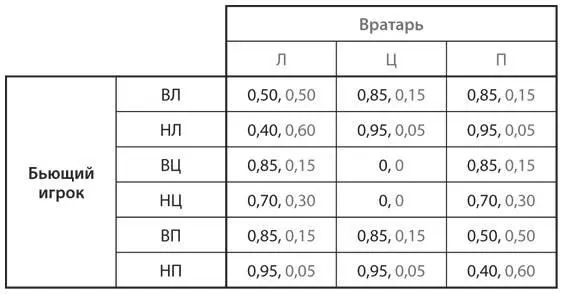
Ваша задача — подтвердить, что в равновесии в смешанных стратегиях данной игры вратарь использует каждую из стратегий Л и П в 42,2 % случаев, а стратегию Ц в 15,6 % случаев, тогда как бьющий игрок применяет каждую из стратегий НЛ и НП в 37,8 % случаев, а стратегию ВЦ в 24,4 % случаев.

a) С учетом предложенной смешанной стратегии вратаря вычислите ожидаемый выигрыш бьющего игрока от каждой из его шести чистых стратегий и с учетом предложенной смешанной стратегии бьющего игрока ожидаемый выигрыш вратаря от каждой из его трех стратегий. (Для простоты используйте только три значащие цифры.)

b) На основании ответа, полученного в пункте а, объясните, почему смешанная стратегия вратаря — наилучший ответ на предложенную смешанную стратегию бьющего игрока и наоборот.

c) Воспользовавшись полученными выше ответами, объясните, почему предложенные стратегии образуют равновесие Нэша.

d) Вычислите равновесный выигрыш игрока, выполняющего пенальти.

S13 (дополнительное упражнение).В разделе 5.Бв контексте игры в доверие мы показали, что изменение выигрышей Салли не меняет пропорций, в которых она смешивает чистые стратегии в равновесии, — ее равновесная комбинация зависит только от выигрышей Гарри. В данном упражнении вам предстоит доказать, что это общий результат для всех равновесий в смешанных стратегиях в играх два на два. Рассмотрим общий случай игры с ненулевой суммой два на два, таблица выигрышей которой представлена ниже.

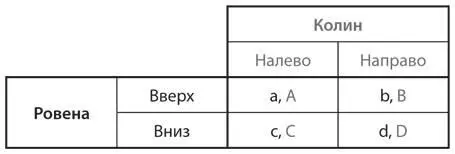
a) Предположим, в этой игре есть равновесие в смешанных стратегиях. Определите вероятность того, что Ровена выберет в равновесии стратегию «вверх» как функцию приведенных в таблице выигрышей.

b) Определите вероятность того, что Колин выберет стратегию «налево» в равновесии.

c) Объясните, как полученные вами результаты показывают, что равновесные комбинации каждого игрока зависят только от выигрышей другого игрока.

d) Каким условиям должны удовлетворять выигрыши, чтобы в данной игре действительно присутствовало равновесие в смешанных стратегиях?

S14 (дополнительное упражнение).Вспомните упражнение S13 из главы 4, основанное на сцене в баре из фильма «Игры разума». Здесь мы проанализируем равновесия в смешанных стратегиях в этой игре, когда в нее играют n > 2 молодых людей.

a) Начните с рассмотрения симметричного случая, когда каждый из n молодых людей самостоятельно пытается привлечь внимание одинокой блондинки с вероятностью P , зависящей от условия, согласно которому каждому молодому человеку должно быть безразлично, какую из двух чистых стратегий выбрать — «блондинка» или «брюнетка», с учетом того, что все остальные игроки смешивают стратегии. Какое условие гарантирует безразличие каждого игрока? Найдите равновесное значение P в этой игре.