Авинаш Диксит - Стратегические игры

U10.Рассмотрите измененную версию игры «камень, ножницы, бумага», в которой Барт получает приз, когда выигрывает, применив стратегию «камень». Если Барт выберет «камень», а Лиза — «ножницы», он получит в два раза больше очков по сравнению с тем, что оба получили бы при любом ином подходе. Новая матрица выигрышей выглядит так:

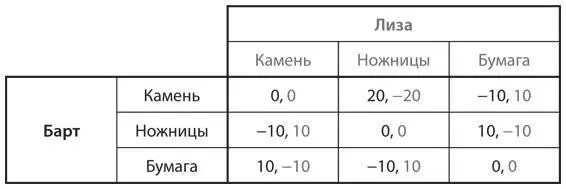
a) Найдите равновесие в смешанных стратегиях в этой версии игры.

b) Сравните полученный результат с равновесием в смешанных стратегиях из упражнения S10. Как вы можете объяснить различия между ними?

U11.Рассмотрите следующую игру.

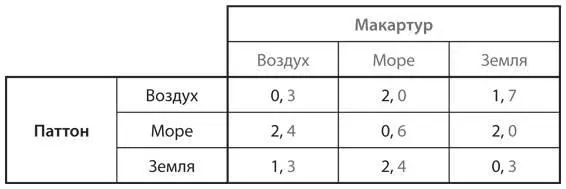
a) Есть ли в ней равновесие в чистых стратегиях? Если да, то какое?

b) Найдите равновесие в смешанных стратегиях в этой игре.

c) В действительности в этой игре два равновесия в смешанных стратегиях. Найдите то, которое вы не нашли в пункте b. (Подсказка: в одном из этих равновесий один из игроков выбирает смешанную стратегию, тогда как другой — чистую.)

U12.Упрямые Джеймс и Дин снова играют в более опасный вариант игры в труса (см. упражнение S6). Они заметили, что их выигрыш («храбрец») зависит от количества зрителей. Чем их больше, тем больше славы и похвал получает тот, кто едет прямо. Безусловно, в случае меньшего количества зрителей наблюдается противоположный эффект. Пусть k > 0 — это выигрыш игрока, который показал себя «храбрецом». Теперь эту игру можно представить так:

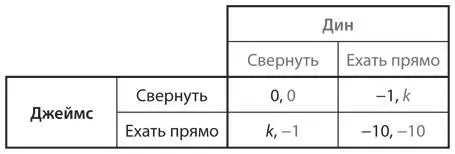
a) С какой вероятностью, выраженной через k , каждый водитель выбирает стратегию «свернуть» в равновесии Нэша в смешанных стратегиях? Применяют ли Джеймс и Дин эту стратегию чаще или реже по мере увеличения значения k ?

b) Чему равна ожидаемая ценность игры для каждого игрока, выраженная через k , в равновесии Нэша в смешанных стратегиях, найденном в пункте а?

c) При каком значении k и Джемс, и Дин смешивают в данном равновесии стратегии в соотношении 50 на 50?

d) Насколько большим должно быть значение k , чтобы средний выигрыш был положительным при схеме чередования, о которой шла речь в пункте с упражнения S6?

U13 (дополнительное упражнение).Вспомните игру из упражнения S11в главе 4, где Ларри, Мо и Керли могут покупать билеты с возможностью получить приз в размере 30 долларов. Мы нашли в ней шесть равновесий Нэша в чистых стратегиях. В данном упражнении вам предстоит найти симметричное равновесие в смешанных стратегиях.

a) Исключите слабо доминируемую стратегию каждого игрока. Объясните, почему игрок никогда не использовал бы ее в своей равновесной комбинации стратегий.

b) Найдите равновесие в смешанных стратегиях.

U14 (дополнительное упражнение).В упражнении S4и упражнении U4показано, что в играх с нулевой суммой, таких как соперничество Эверт и Навратиловой в теннисе, изменение выигрышей одного игрока иногда приводит к неожиданным или парадоксальным изменениям в равновесной комбинации стратегий. Но что происходит при этом с ожидаемой ценностью игры? Рассмотрим следующую общую форму игры с нулевой суммой с участием двух игроков:

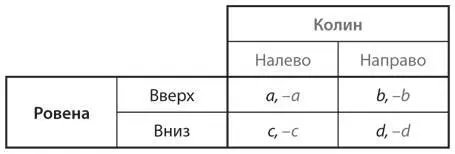
Предположим, в этой игре нет равновесия Нэша в чистых стратегиях, а значения a, b, c и d больше или равны 0. Может ли увеличение значения одной из переменных a, b, c и d обусловить снижение ценности игры для Ровены? Если нет, докажите это. Если да, приведите пример.

При вычислении ожидаемых выигрышей и равновесий в смешанных стратегиях в данной главе мы должны были выполнить ряд простых действий с вероятностями. Для этого существует несколько несложных правил. Возможно, многие из вас с ними знакомы, но мы дадим здесь краткое описание и объяснение основных понятий, чтобы вы могли в случае необходимости восстановить или восполнить свои знания. Кроме того, мы также покажем, как вычислить математическое ожидание случайных числовых величин.

Базовое интуитивное представление вероятности наступления того или иного события формируется в процессе размышлений о частоте, с которой оно происходит случайно в рамках более крупного множества возможных событий. Как правило, любой элемент более крупного множества столь же вероятен, как и любой другой элемент. Следовательно, поиск вероятности интересующего нас события сводится к подсчету числа элементов, соответствующих этому событию, и их делению на общее количество элементов в крупном множестве [111].

Например, в любой стандартной колоде из 52 игральных карт четыре масти (трефы, бубны, червы и пики), по 13 карт разного достоинства в каждой: сначала туз, затем номерные карты от 2 до 10 и фигурные карты — валет, дама, король. Мы можем задать массу разных вопросов о том, с какой вероятностью из данной колоды карт можно извлечь карту определенной масти или достоинства (или масти и достоинства): с какой вероятностью можно вытащить карту пиковой масти? А черную карту? А десятку? А даму пик? И так далее. Чтобы ответить на эти вопросы, необходимо обладать определенными знаниями о вычислении вероятностей и о действиях с ними. Если бы у нас было две колоды карт (одна с синими рубашками, а другая с зелеными), мы могли бы задать еще более сложные вопросы («С какой вероятностью можно вытащить по одной карте из каждой колоды так, чтобы обе карты оказались валетом бубен?»), но для получения ответа на них по-прежнему использовали бы все те же алгебраические действия с вероятностями.

В широком смысле вероятность— это степень возможности наступления определенного события или совокупности событий. Возможность того, что вы извлечете карту пиковой масти из колоды карт, — просто вероятность наступления события «вытащить пику». В данном случае крупное множество содержит 52 элемента (общее количество в равной степени вероятных возможностей), а событие «вытащить пику» соответствует подмножеству, состоящему из 13 конкретных элементов. Таким образом, у вас есть 13 шансов из 52 вытащить пику, а значит, вероятность сделать это за один раз равна 13/52 = 1/4 = 25 %. Данную ситуацию можно представить себе иначе: у вас есть четыре масти по 13 карт в каждой, следовательно, ваш шанс извлечь карту определенной масти составляет один к четырем, или 25 %. Если бы вы тащили карту несколько раз (каждый раз из полной колоды карт), то из 52 попыток вы не всегда вытаскивали бы пику в точности 13 раз; по воле случая вы порой вытаскивали бы на несколько больше, а иногда на несколько меньше пик. Однако когда извлечение карт из колоды выполняется многократно, существуют разные множества из 52 попыток и этот шанс усредняется. В таком случае вероятность 25 % представляет собой среднее значение частоты вытаскивания карты пиковой масти в большом количестве наблюдений [112].