Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Решив одну задачу о птицах, вы сможете решить их все; для этого необходимо просто записать условия в виде системы уравнений и найти ответ в виде целых чисел.

Во многих других головоломках ситуацию также следует представить как систему уравнений. Как правило, в них не хватает уравнений для всех переменных, поэтому при решении приходится полагаться на тщательно продуманный метод проб и ошибок или математическое озарение. Следующая задача – моя любимая, причем не только потому, что количество данных кажется невероятно скудным (всего два уравнения на четыре переменные), но и потому, что фигурирующее в ней число имеет непосредственное отношение к известному бренду.

Ответ

[22]

Покупатель заходит в магазин 7-Eleven и покупает несколько товаров.

– С вас 7,11 фунта, – говорит кассир.

– Забавно… – отвечает покупатель.

– Да, – говорит кассир, – я только перемножил цены этих четырех товаров.

– А разве вы не должны были их сложить?

– Согласен, но сумма цен дает то же число.

Сколько стоит каждый товар?

Для решения задачи нужно знать пару простых математических фактов. Во-первых, простое число – это целое число, которое делится только на себя и на 1. Список простых чисел начинается так:

2, 3, 5, 7, 11, 13, 17, 19…

Во-вторых, нужно знать основную теорему арифметики и, самое важное, главное правило простых чисел, а именно: каждое целое число можно представить в виде произведения уникального множества простых чисел. Например:

60 = 2 × 2 × 3 × 5

711 = 3 × 3 × 79

123 456 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 643

В каждом случае число можно разбить на простые множители только одним способом. Возможно, вы принимали это правило как нечто само собой разумеющееся, даже не зная его названия. Как бы там ни было, основная теорема арифметики поможет вам составить одно из уравнений, необходимых для решения данной задачи.

Для деления больших чисел на простые множители вам может понадобиться калькулятор или компьютер. Но даже несмотря на это, задача остается невероятно увлекательной.

Что связывает великого математика XIX столетия Симеона Дени Пуассона с актером Брюсом Уиллисом, героем голливудских боевиков? Оба решили представленную ниже головоломку. Биограф Пуассона писал, что эта головоломка стала той искрой, которая разожгла интерес юного француза к математике. «Без всяких размышлений о таких вещах, не зная ни условных обозначений, ни алгебраических методов, без какой-либо предварительной подготовки он решил [ее] самостоятельно – и в тот самый день почувствовал, что в нем родилась любовь к математике, от которой он не должен отказываться. Так начался его путь к славе». Браво!

На Брюса Уиллиса эта головоломка повлияла столь же жизнеутверждающе. В фильме «Крепкий орешек 3: Возмездие» он и актер Сэмюэл Джексон решили эту задачу, чтобы обезвредить бомбу с часовым механизмом. Если это смогли сделать Уиллис и Джексон, сможете и вы.

Ответ

У вас есть 8-литровый кувшин с вином и два пустых кувшина емкостью 5 и 3 литра. Ни на одном из них нет мерной шкалы.

Налейте в один из кувшинов ровно 4 литра вина.

Впервые эта задача появилась в летописи XIII века аббата Альберта из городка Штаде близ Гамбурга. Этот опус включает самое подробное описание средневекового похода паломников из Северной Европы в Рим, написанное в форме диалога между двумя странствующими монахами Тирри и Фирри. В их шутливых беседах содержится несколько головоломок. «Раздели вино, – говорит Тирри Фирри, поддразнивая его задачей с тремя кувшинами, – иначе останешься без ничего».

Решать эту головоломку действительно весело, и я предоставляю вам возможность сделать это обычным способом, то есть, переливая вино из одного кувшина в другой, посмотреть, чем это закончится. Сделайте это, прежде чем продолжите читать.

Теперь я покажу вам другой способ решения задачи о трех кувшинах, используя шары, перемещающиеся по бильярдному столу необычной формы.

Бильярдный стол (см. рисунок) представляет собой параллелограмм со сторонами пять и три единицы, состоящий из равносторонних треугольников. Я обозначил их на рисунке, поскольку эти треугольники образуют систему координат ( x, y ). В ней значения x расположены по горизонтали, а y – по диагонали.

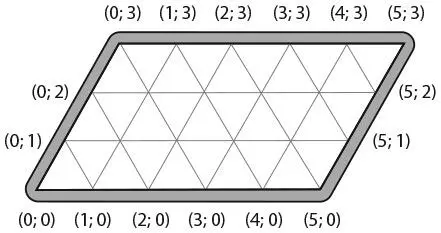
На следующем рисунке показано, что произойдет, если поместить шар в позицию с координатой (5; 0) и отправить его вдоль стороны треугольника. Шар отскочит от стенок бильярдного стола в точках (2; 3), (2; 0), (0; 2), (5; 2) и (4; 3), прежде чем двинется дальше. (Математические бильярдные столы лишены трения, поэтому шары перемещаются в том направлении, в каком вы их отправляете.)

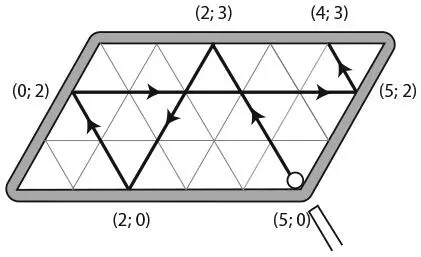
А теперь рассмотрим удар по шару, расположенному в точке (0; 3). Он отскочит от стенок в точках (3; 0), (3; 3), (5; 1), (0; 1), (1; 0), (1; 3) и (4; 0), прежде чем продолжит свой путь.

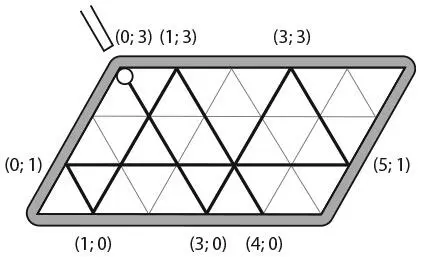
Давайте тщательнее проанализируем эти координаты:

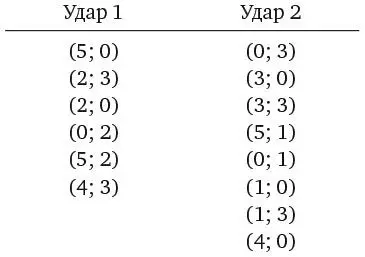
Не кажутся ли вам эти числа знакомыми? Надеюсь, что да! Ведь это и есть два возможных решения задачи о трех кувшинах.

Для того чтобы не запутаться, обозначим 5-литровый кувшин буквой A, а 3-литровый буквой Б.

Сначала оба кувшина пусты.

Наполним кувшин А. Состояние кувшинов такое: А = 5 литров, Б = 0 литров. Запишите это значение как (5; 0).

Теперь перелейте жидкость из кувшина А в кувшин Б. В кувшине А остается 2 литра, а кувшин Б полон, то есть в нем 3 литра. Кувшины находятся в точке (2; 3).

Вылейте жидкость из кувшина Б в третий кувшин. Теперь кувшины в точке (2; 0).

Перелейте жидкость из кувшина А в кувшин Б: (0; 2).

Снова наполните кувшин А: (5; 2)

Перелейте жидкость из кувшина А в кувшин Б: (4; 3).

Все: в кувшине А 4 литра, а значит, задача решена.

Объем жидкости в кувшинах А и Б в точности соответствует координатам точек, в которых шар отскакивает от стенок бильярдного стола после удара из точки (5; 0).

Если бы при поиске решения головоломки мы сначала наполнили кувшин Б, то объем жидкости в кувшинах А и Б можно было бы описать координатами точек, в которых шар отскакивает от стенок бильярдного стола после удара из позиции (0; 3).