Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Метод решения задач с кувшинами посредством шаров открыл британский статистик Морис Твиди в 1939 году, когда ему было двадцать лет. Каждый раз, когда шар отскакивает от стенок ромбовидного стола, траектория его движения приводит вас к следующему действию.

Если вам когда-либо понадобится вылить определенное количество жидкости из полной посуды в две пустые емкости поменьше без мерной шкалы, объем которых равен х и y , все, что вам нужно будет сделать, – это построить ромбовидный бильярдный стол со сторонами х и y и катать по нему шары.

Господа Уиллис и Джексон, если вы читаете эти строки, примите мои слова к сведению.

Ответ

Вы стоите у ручья с двумя ведрами вместимостью семь и пять галлонов. Как набрать шесть галлонов воды за минимальное количество переливаний?

Идея переливания жидкости из одного сосуда в другой лежит в основе ряда других занимательных головоломок.

Ответ

В термосе у вас кофе, в чашке – молоко. Вы налили некоторое количество кофе в чашку с молоком, а затем перелили немного напитка назад в термос так, чтобы уровень жидкости в обеих емкостях был таким же, как изначально.

Чего больше – кофе в чашке или молока в термосе?

Эта задача вам на завтрак, а следующая предназначена для более позднего времени дня.

Ответ

У вас есть пинта воды в одном кувшине и пинта вина в другом. Вылейте полпинты воды в вино и перемешайте. В кувшине с вином теперь пинта вина и полпинты воды. Вылейте полпинты разбавленного вина в кувшин с водой так, чтобы в каждом кувшине оказалось по одной пинте жидкости. Перемешайте. Продолжайте переливать по полпинты из одного кувшина в другой.

После скольких переливаний в двух кувшинах будет одинаковое содержание вина в жидкости?

Жидкость не единственное вещество, которое льется. Примерно таким же свойством обладает песок. Ниже представлен вариант задачи с кувшинами, в котором необходимо измерять время, а не объем.

Ответ

С помощью песочных часов на 7 и 11 минут отмерьте ровно четверть часа.

Я помогу вам решить эту задачу. Итак, у нас есть пара песочных часов и мы будем их переворачивать. Перевернув одни часы, мы смогли бы отмерить только либо 7, либо 11 минут, то есть вернулись бы к тому, с чего начали.

Давайте проанализируем числа – это полезно. Наши песочные часы отмеряют 7 и 11 минут, а нам необходимо отмерить 15 минут. Разность между одиннадцатью и семью равна четырем, а это то же число, что и разность между пятнадцатью и одиннадцатью. Значит, при решении нам нужно придерживаться следующей стратегии.

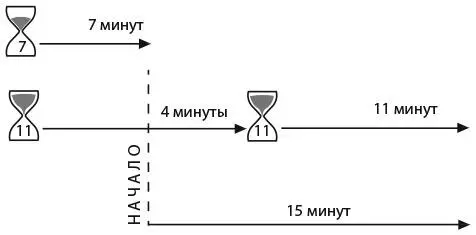
Переверните двое часов. Через семь минут в 7-минутных часах упадут последние песчинки, а вторые часы будут отсчитывать время еще 4 минуты. Именно этот интервал нам и нужен: здесь начнем отсчет 15 минут. Через четыре минуты 11-минутные часы опустеют. Сразу же переверните их – и через 11 минут получите ровно 15 минут, как показано на рисунке.

Впрочем, это не самое лучшее решение, ведь на него у нас ушло целых 22 минуты, хотя отмерить надо было четверть часа. Найдите более подходящий способ.

Измерять время можно и с помощью фитиля.

Ответ

У вас есть набор фитилей, каждый из которых сгорает за один час. Длинные и тонкие фитили горят неравномерно: один участок может гореть быстрее, чем другой. Разрезание фитиля пополам не гарантирует, что каждая половина сгорит за полчаса.

1. С помощью двух фитилей отмерьте 45 минут.

2. С помощью одного фитиля как можно точнее отмерьте 20 минут.

Соль этой задачи в том, что понимание математики позволяет исключить условие неравномерности горения и точно отмерить промежутки времени. Мне нравится, что в этой головоломке математика берет верх над физикой.

Ниже предложена еще одна головоломка о том, как преодолеть несовершенство физического мира.

Ответ

В случае подбрасывания обычной монеты вероятность выпадения орла или решки равна 50: 50. Допустим, ваша монета с дефектом, из-за чего вероятность выпадения орла или решки составляет не 50: 50, а какое-то другое соотношение. Можно ли сделать так, чтобы она вела себя как обычная монета? Необходимо найти такую комбинацию подбрасываний, которая обеспечит результат 50: 50.

Монеты – важнейший инструмент в мире головоломок; в следующей главе мы поговорим о них подробнее.

Рычажные весы были единственным инструментом для взвешивания предметов вплоть до XVIII столетия, когда были изобретены пружинные весы с одной чашей. Будучи распространенным измерительным прибором, рычажные весы часто были героями математических головоломок, начиная с эпохи Возрождения до эпохи Просвещения и позднее. Решите одну из них.

Ответ

У вас есть рычажные весы и две гири весом 10 и 40 граммов. Разделите 1 килограмм муки на две части – 200 и 800 граммов – за три взвешивания.

Предположим, у нас есть набор килограммовых гирь, соответствующих первым шести членам последовательности удваивающихся чисел: 1, 2, 4, 8, 16, 32. Комбинируя эти шесть гирь, можно получить любой вес от 1 до 63 килограммов. Например:

3 = 2 + 1.

Другими словами, для того чтобы получить 3 килограмма, необходимо взять две гири весом 2 и 1 килограмм.

13 = 8 + 4 + 1;

27 = 16 + 8 + 2 + 1;

63 = 32 + 16 + 8 + 4 + 2 + 1.

В действительности шесть гирь образуют минимальный набор , позволяющий измерить любой вес в килограммах от 1 до 63.

Почему это так, можно понять, рассматривая выражение веса в двоичных числах. В двоичной системе счисления используются только цифры 1 и 0. Двоичные числа – это числа десятичной системы, записанные с помощью 1 и 0: 1, 10, 11, 100, 110 и т. д. Числа 1, 10, 100, 1000, 10 000 и 100 000 в двоичной системе счисления соответствуют десятичным числам 1, 2, 4, 8, 16 и 32. Таким образом, двоичные числа – это своего рода инструкции в отношении того, как выстраивать числа с помощью последовательности, в которой каждый очередной член в два раза больше предыдущего. Таким образом, в двоичной системе следующие числа записываются так:

3 – это 11

13 – 1101

27 – 11 011

63 – 111 111

Цифра 1 в крайнем правом столбце соответствует 1, цифра 1 в соседнем столбце – 2, цифра 1 в следующем столбце – 4 и т. д. Аналогичным образом цифра 0 в крайнем правом столбце означает отсутствие цифры 1, цифра 0 в соседнем столбце означает отсутствие цифры 2, цифра 0 в следующем столбце – отсутствие цифры 4 и т. д.

Итак, возьмем число 13, которое записывается в двоичной системе как 1101. Эта группа цифр справа налево означает: одна цифра 1, нет цифры 2, одна цифра 4 и одна цифра 8. Другими словами, 13 = 1 + 4 + 8 – как и было сказано.