Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Как и в большинстве алгебраических задач, первым делом следует перевести всю имеющуюся информацию в символы. Поскольку длина и ширина коробки равны x , то их сумма составит 2 x . А учитывая, что высота плюс ширина плюс длина не могут превышать 45 дюймов [167], на высоту остается 45 – 2 x дюймов. Таким образом, объем коробки равен x × x × (45 – 2 x ) кубических дюймов. В результате умножения получаем 45 x 2 – 2 x 3. Это и есть объем коробки. Обозначим его V ( x ). Итак,

V ( x ) = 45 x 2 – 2 x 3.

Если мы сейчас на мгновение сжульничаем и с помощью компьютера построим график, отложив x по горизонтали, а V по вертикали, то увидим, как кривая возрастает и достигает максимума при x = 15 дюймов, как и ожидалось, а потом снова спускается к нулю.

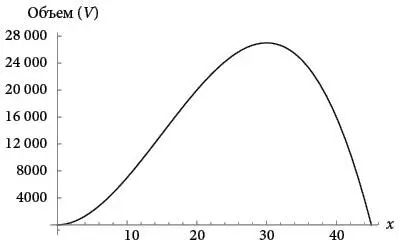
Широко используемый сегодня альтернативный способ найти это максимальное значение с помощью дифференциального исчисления – вычислить производную функции V ( x ) и приравнять ее к нулю. В верхней точке кривой угол наклона равен нулю: кривая тут не поднимается и не опускается. Поэтому, если определять наклон через производную (как мы увидим в главе 6), то в точке максимума она должна быть равна 0. Немного алгебры и применения различных правил для производных – и мы получим для точки максимума то же самое значение x = 30.

Однако у Ферма не было компьютеров и графопостроителей, и, конечно же, он не оперировал понятием производной; наоборот, выдвинутые им идеи и привели к производным! Так как же он решал эту задачу? Он использовал особое свойство максимума: горизонтальная линия ниже максимума пересекает кривую в двух точках, как показано ниже, в то время как горизонтальные линии выше максимума вообще не пересекают кривую.

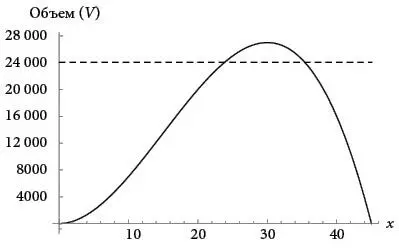
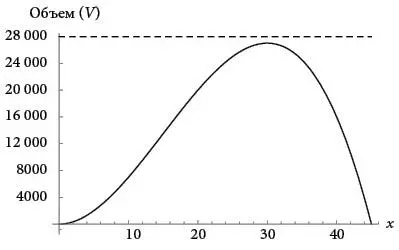
Это подсказывало интуитивную стратегию решения задачи. Представьте, что вы медленно поднимаете горизонтальную линию, начиная ниже максимума. По мере ее постепенного перемещения вверх две точки пересечения с кривой двигаются по ней навстречу друг другу, словно бусины в ожерелье.

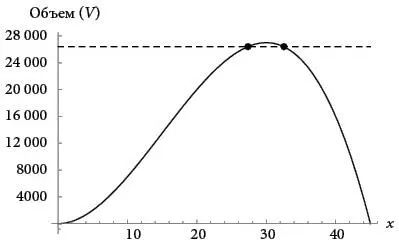
В максимуме эти две точки сливаются. Наблюдение за их слиянием и позволило Ферма определить максимум. Он вывел условие, при котором две точки сливаются в одну, образуя так называемое двойное пересечение . С такой идеей все остальное – чистая алгебра, простое манипулирование символами. Это выглядит так.

Предположим, что наши два пересечения происходят в точках x = a и x = b . Тогда, поскольку по построению точки пересечения находятся на одной горизонтальной линии, должно быть справедливо V ( a ) = V ( b ). Следовательно,

45 a 2 – 2 a 3 = 45 b 2 – 2 b 3.

Теперь полезно перегруппировать слагаемые. Перенесем квадраты в одну часть, а кубы в другую и получим

45 a 2 – 45 b 2 = 2 a 3 – 2 b 3.

Вспомнив школьную алгебру, разложим обе части на множители и получим

45( a – b )( a + b ) = 2( a – b )( a 2 + ab + b 2).

Разделим обе части на общий множитель a – b . Это корректное действие, поскольку предполагается, что a и b различны (если бы они были одинаковыми, то деление на a – b означало бы деление на 0, что запрещено, как мы говорили в главе 1). В результате получим уравнение

45( a + b ) = 2( a 2 + ab + b 2).

А теперь напрягитесь, чтобы разобраться в несколько смущающем логическом выводе. Ферма только что предполагал, что a и b не равны, но тем не менее утверждает, что выведенное уравнение останется верным, когда a и b станут равными – при слиянии в максимуме. Он пытается оправдать это соображение, прибегая к туманному понятию «квазиравенства» [168](«приближенного равенства», adaequalitas ). Оно выражает идею, что a и b в точке максимума становятся в определенном смысле равными, но равными не по-настоящему (сегодня мы бы это сформулировали с помощью понятия предела или бесконечной близости). В любом случае он принимает a ≈ b , где знак означает приближенное равенство, а затем бесцеремонно подставляет a вместо b в вышеуказанное уравнение и получает

45(2 a ) = 2( a 2 + a 2 + a 2).

Это уравнение упрощается до 90 a = 6 a 2, откуда получаются два решения: a = 0 и a = 15. Первое, a = 0, дает коробку минимального объема с нулевой длиной и шириной, а значит и объем ее равен 0. Второе, a = 15, дает коробку максимального объема – как раз тот ответ, который мы и ожидали: оптимальная ширина и длина составляют по 15 дюймов.

С современной точки зрения рассуждения Ферма кажутся странными. Он находит максимум, не прибегая к производным. Сегодня, прежде чем решать задачи на оптимизацию, мы изучаем производные; Ферма поступал наоборот. Но это не имеет значения. Его идеи эквивалентны нашим.

Как Ферма помог ФБР

Наследие первых работ Ферма по оптимизации окружает нас повсюду. Наша нынешняя жизнь зависит от алгоритмов, которые решают задачи оптимизации с помощью условий, выражаемых производными. Современные задачи, как правило, намного сложнее, чем у французского математика, но дух остается тем же.

Одно важное применение касается больших массивов данных, когда их полезно кодировать как можно компактнее. Например, в базе ФБР миллионы отпечатков пальцев. Для их хранения, поиска и эффективного извлечения эта организация использует методы сжатия данных, основанные на анализе. Умные алгоритмы уменьшают размеры файлов с оцифрованными отпечатками без ущерба для важных деталей. То же самое верно при хранении нами на телефоне музыки или изображений. Вместо того чтобы сохранять каждую ноту и каждый пиксель, алгоритмы сжатия, используемые в форматах MP3 и JPEG [169], экономят место за счет преобразования информации в более эффективную форму. Они также позволяют нам быстро загружать песни и фотографии и отправлять их нашим близким, не слишком забивая их почтовые ящики.

Чтобы понять, какое отношение анализ и оптимизация имеют к сжатию данных, давайте рассмотрим статистическую задачу подбора какой-либо кривой, наилучшим образом соответствующей определенным данным, – задачу, которая возникает повсюду, от климатологии до бизнес-прогнозирования. Изучим данные, показывающие, как изменяется продолжительность дня в зависимости от времени года [170]. Как мы знаем, летом дни длиннее, а зимой короче, но как выглядит общая закономерность? На приведенном ниже графике я отобразил сведения для Нью-Йорка за 2018 год, отложив по горизонтальной оси время от 1 января слева до 31 декабря справа. Вертикальная ось показывает количество минут между рассветом и закатом в разное время года. Чтобы не загромождать картинку, я показал только точки для 27 дней – через каждые две недели, начиная с 1 января.