Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Все это приводит к крайне важному общему выводу: именно закономерности в первую очередь и обеспечивают сжатие. Сжать можно только данные, следующие какому-то шаблону. Со случайными данными это не получится. К счастью, многие вещи, которые интересны людям – отпечатки пальцев, песни и лица, – хорошо структурированы и обладают закономерностями. Подобно тому как продолжительность дня следует простой синусоиде, фотография лица включает брови, дефекты кожи, скулы и прочие характерные признаки. В песнях есть мелодия, гармония, ритмы и динамика. В отпечатках имеются гребни, петли и завитки. Будучи людьми, мы мгновенно распознаем эти закономерности. Компьютеры тоже можно научить их распознавать. Синусоиды идеально подходят для отображения периодических закономерностей, но менее пригодны для представления более резко локализованных особенностей, таких как края ноздрей или родинок.

Для этой цели исследователи, работающие в различных областях, придумали кривые, которые называются вейвлетами [171]. Эти маленькие волны более локализованы, чем синусоиды. Они не распространяются в обоих направлениях, а сильно сконцентрированы во времени и пространстве.

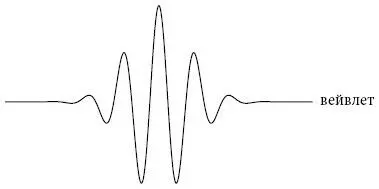
Вейвлеты внезапно появляются, несколько раз колеблются, а затем исчезают. Они похожи на сигналы кардиомониторов или всплески активности, регистрируемые сейсмографами при землетрясениях. Они идеально подходят для изображения резкого всплеска при регистрации мозговых волн, толстого мазка на картине Ван Гога или морщины на лице.

ФБР использовало вейвлеты [172]для преобразования файлов с отпечатками пальцев. Со времени внедрения практики применения отпечатков в начале XX века они хранились в виде чернильных оттисков на бумажных носителях. К середине 1990-х фонды разрослись примерно до двух миллионов карточек и занимали почти половину гектара офисных площадей. Когда ФБР решило оцифровать эти досье, специалисты превратили их в полутоновые изображения с 256 уровнями серого цвета и разрешением в 500 точек на дюйм, вполне достаточным для улавливания всех мелких завитков, петель, краев гребней, разветвлений и прочих идентифицирующих деталей.

Проблема, однако, заключалась в том, что в то время на одной оцифрованной карте содержалось примерно 10 мегабайт данных, что делало невозможной быструю отправку таких файлов местным полицейским участкам. Не забывайте, что это происходило в середине 1990-х, когда самыми передовыми технологиями были модемы и факсы, а передача 10-мегабайтного файла занимала часы. К тому же обмениваться такими файлами, когда в качестве носителей чаще всего применялись дискеты на 1,5 мегабайта, достаточно трудно. Растущие требования по ускорению обработки ежедневно появляющихся тридцати тысяч новых карт с отпечатками и запросов о срочных проверках привели к острой необходимости модернизации системы. ФБР нуждалось в способе сжать файлы без искажений.

Вейвлеты идеально подходили для такой работы. Представляя отпечатки в виде комбинаций множества вейвлетов и оптимально регулируя соответствующие ручки с помощью анализа, математики из Лос-Аламосской национальной лаборатории помогли ФБР [173]уменьшить файлы больше чем в двадцать раз. Это была революция в криминалистике. Благодаря идеям Ферма в современной форме (в сочетании с еще большей ролью вейвлет-анализа, информатики и обработки сигналов) 10-мегабайтный файл можно было сжать всего лишь до 500 килобайт, то есть до размера, вполне пригодного для отправки по телефонным линиям. И это можно было сделать, не жертвуя достоверностью. Эксперты-дактилоскописты высказали свое одобрение. То же самое сделали и компьютеры: сжатые файлы триумфально прошли через автоматическую систему идентификации ФБР. Это были хорошие новости для анализа и плохие – для преступников.

Принцип наименьшего времени

Интересно, что бы подумал Ферма о таком использовании своих идей? Он никогда особо не интересовался прикладной математикой. Ему нравилось заниматься наукой из любви к ней. Тем не менее он внес в прикладную математику один вклад непреходящей важности: первым вывел закон природы из более глубокого закона, используя анализ в качестве логического двигателя. Точно так же как Максвелл сделает с электричеством и магнетизмом два столетия спустя, Ферма перевел гипотетический закон природы на язык анализа, запустил двигатель, ввел в него один закон и получил на выходе другой как следствие первого. Сделав это, Ферма, бессистемный ученый, положил начало стилю рассуждений, который с тех пор доминирует в теоретической науке.

История началась в 1637 году, когда группа парижских математиков заинтересовалась мнением Ферма о последнем трактате Декарта, посвященном оптике. Декарт придерживался определенной теории о том, как изгибается луч света при попадании из воздуха в воду или из воздуха в стекло (эффект, известный как преломление).

Любой, кто когда-нибудь играл с увеличительным стеклом, знает, что свет можно фокусировать, а направление луча – менять. В детстве мне нравилось поджигать листья на дорожке с помощью лупы: я поднимал и опускал ее, пока солнечные лучи не фокусировались в белое пятно большой яркости, из-за чего листья тлели и в итоге загорались. Менее зрелищным образом преломление используется в очках. Линзы в очках фокусируют лучи света так, чтобы они оказывались в нужном месте сетчатки – для исправления дефектов зрения.

Отклонение луча также объясняет иллюзию, которую вы, возможно, наблюдали у плавательного бассейна в солнечный день. Предположим, что на дне бассейна находится некий блестящий предмет, скажем ювелирное украшение.

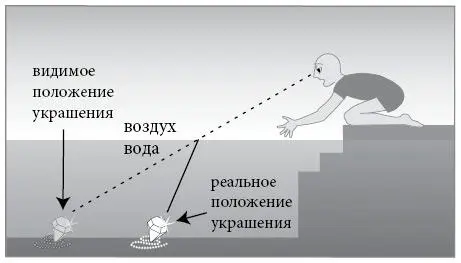
Вы смотрите на предмет через воду, но он оказывается совсем не там, где кажется, поскольку отраженные от него солнечные лучи преломляются на обратном пути из бассейна, переходя из воды в воздух. По той же причине рыбак, охотящийся на рыбу с острогой, должен целиться ниже ее видимого положения, чтобы попасть в нее.

Такие феномены преломления подчиняются простому правилу. Когда луч света переходит из менее плотной среды (например, воздуха) в более плотную (воду или стекло), он меняет направление в сторону перпендикуляра между двумя средами. А при переходе из более плотной среды в менее плотную луч отклоняется от этого перпендикуляра, как показано на рисунке.

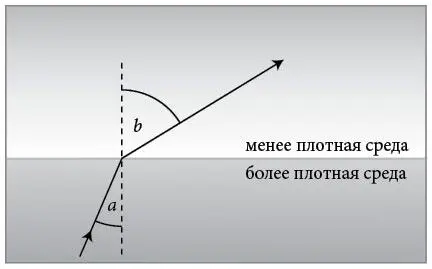
В 1621 году голландский ученый Виллеброрд Снелл уточнил это правило и выразил его количественно, проведя простой эксперимент. Меняя угол a входящего луча и наблюдая, как в результате меняется угол b выходящего луча, он обнаружил, что отношение sin a / sin b для конкретной пары сред всегда остается постоянным. (Здесь sin обозначает синус – ту самую тригонометрическую функцию, волнистый график которой мы рассматривали при изучении продолжительности дня.)