Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

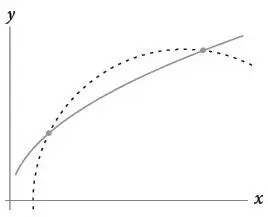
Меняя положение и радиус окружности, Декарт заставлял две точки пересечения сливаться в одну. В итоге окружность касалась кривой – бинго!

Это давало ученому возможность найти касательную к кривой. Одновременно у него получалась нормаль к кривой – прямая, перпендикулярная касательной в точке касания; по ней идет радиус построенной окружности.

Метод Декарта был верным, но неуклюжим. Приходилось производить массу вычислений, гораздо больше, чем в методе Ферма. Однако Декарт тогда даже не слышал о Ферма, поэтому в своей обычной самоуверенной манере полагал, что превзошел всех. В «Геометрии» он хвалился: «Я дам общий способ проведения прямых, пересекающих под прямыми углами кривые линии в любых точках. И я смею сказать, что эта задача является наиболее полезной и общей не только среди известных мне, но также среди всех тех задач, которые я когда-либо желал знать в геометрии» [180], [181].

Позднее, в 1637 году, когда Декарт узнал от своих корреспондентов в Париже, что Ферма опередил его в решении задачи о касательной примерно на десять лет, хотя так и не удосужился опубликовать его, он встревожился. В 1638 году он изучил метод Ферма, ища в нем дыры. Конечно же, их было много! В письме одному посреднику Декарт заявлял: «Я даже не хочу называть его имени, чтобы он не стыдился тех ошибок, что я обнаружил» [182]. Он оспаривал логику Ферма, которая, честно говоря, была расплывчатой и плохо объясненной. Но в конце концов, после обмена несколькими письмами, в которых Ферма спокойно пытался объяснить свои идеи, Декарт был вынужден согласиться, что рассуждения оппонента верны.

Однако, прежде чем признать поражение, он попытался озадачить тулузского математика, предложив ему найти касательную к кривой, определяемой кубическим уравнением x 3 + y 3 = 3 axy , где величина a представляла собой константу. Декарт знал, что с помощью своего неуклюжего метода, использующего окружности, сам он не смог бы ее найти – алгебраические вычисления стали неуправляемыми, поэтому с уверенностью полагал, что и Ферма не справится с задачей с помощью своего метода с применением прямых. Однако Ферма был более сильным математиком и его метод был лучше, поэтому, к немалой досаде Декарта, он разобрался с задачей без особых усилий.

Ферма заложил основы анализа в его современной форме. Его принцип наименьшего времени показал, что оптимизация глубоко вплетена в ткань природы. Работы по аналитической геометрии и касательным проложили путь к дифференциальному исчислению, по которому вскоре последовали другие. А виртуозное владение алгеброй позволило ему определить площади под некоторыми кривыми, которые не смогли найти даже его самые выдающиеся предшественники. В частности, он вычислил площадь под кривой y = x n для любого положительного целого n (другие математики решили задачу для первых девяти случаев, n = 1,2,…,9, однако не смогли найти решение для всех n ) [183]. Прорыв Ферма был колоссальным шагом в сторону интегрального исчисления, который закладывал фундамент для будущих прорывов.

И тем не менее его исследования не дотянули до секрета [184], который вскоре откроют Ньютон и Лейбниц, – секрета, который революционизировал и объединил обе стороны анализа. Жаль, что это не удалось Ферма, ведь он подобрался очень близко. Недостающее звено имело отношение к тому, что он придумал, но не счел важным – нечто скрытое в его методе максимумов и касательных. Позднее это назовут производной. Их использование выйдет далеко за рамки кривых и касательных и включит все виды изменений.

Итак, мы подошли в нашей истории к перекрестку. Именно здесь анализ становится современным и переходит от загадки кривых к изучению загадок движения и изменений. Именно здесь анализ начинает интересоваться ритмами Вселенной, ее взлетами, падениями и закономерностями. Анализ больше не довольствуется статическим миром геометрии: он увлекается динамикой. Он спрашивает: каковы правила движения и изменений? Что мы можем уверенно предсказать о будущем?

За четыре столетия, прошедшие с тех пор, как анализ оказался на этом перекрестке, он ушел от алгебры и геометрии в сторону физики и астрономии, биологии и медицины, инженерии и технологий, то есть во все сферы, где есть нескончаемые перемены. Анализ математизировал время и вселил в нас надежду, что мир, в котором мы живем, при всех его несправедливостях, страданиях и хаосе, глубоко в своем сердце, где он следует математическим законам, может быть разумным. Иногда мы можем найти эти законы с помощью науки. Иногда можем понять их с помощью анализа. А иногда можем использовать, чтобы улучшить нашу жизнь, помочь обществу и изменить ход истории к лучшему.

Поворотный момент в истории анализа произошел в середине XVII века, когда загадки кривых, движения и изменений столкнулись на двумерной сетке – координатной плоскости Ферма и Декарта. В тот момент Ферма и Декарт понятия не имели, насколько универсальный инструмент создали. Они задумывали прямоугольную систему координат для использования в чистой математике. Но с самого начала она тоже стала своего рода перекрестком, где уравнения встречались с кривыми, алгебра – с геометрией, а математики Запада – с коллегами с Востока. Далее, уже в следующем поколении, Исаак Ньютон, опираясь на их работы и на труды Кеплера и Галилея, объединил геометрию и физику в великом синтезе. Искра Ньютона зажгла тот огонь, который дал старт эпохе Просвещения и революции в западной науке и математике.

Однако для изложения этой истории нам нужно начать с арены, где все это происходило, – координатной плоскости. Когда сегодня учащиеся начинают заниматься анализом, они проводят на ней массу времени. Название соответствующего предмета – математический анализ функций одной переменной. Мы займемся этой темой в нескольких следующих главах. Сейчас же начнем с функций.

За столетия, прошедшие с тех пор, как кривые столкнулись с движением и изменениями, важность координатной плоскости существенно увеличилась. Сегодня она применяется везде для графического представления данных и выявления скрытых закономерностей. Мы можем использовать ее, чтобы увидеть, как одна переменная зависит от другой, как соотносятся x и y , когда все остальное постоянно. Такие отношения моделируются с помощью функций одной переменной. Символически это записывается как y = f ( x ), что читается « y равно f от x ». Здесь f обозначает функцию, описывающую, как переменная y (называемая зависимой переменной) зависит от переменной x ( независимой переменной), если предполагается, что все остальное зафиксировано и неизменно. Такие функции моделируют, как ведет себя мир в самом чистом виде. Причина вызывает прогнозируемый результат. Доза вызывает прогнозируемый эффект. Говоря формально, функция f – это правило, по которому каждому значению x сопоставляется некоторое значение y . Это похоже на машину ввода-вывода: на вход подается число x , а на выходе она выдает число y и делает это предсказуемо и надежно.