Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

.

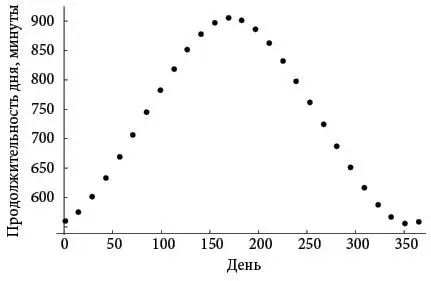
График показывает, что, как и ожидалось, в течение года продолжительность дня увеличивается и уменьшается. Самые длинные дни приходятся на период летнего солнцестояния (21 июня, что соответствует пику около 172-го дня примерно в середине графика), а самые короткие – зимнего солнцестояния, через полгода. В целом же картина напоминает некую плавную волну.

На уроках тригонометрии в школе учителя рассказывают об определенном виде такой кривой – синусоиде. Чуть позже я вам тоже более подробно объясню, что такое синусоида и почему она важна для анализа. А пока нам нужно знать, что синусоида связана с круговым движением. Чтобы увидеть связь, представьте себе точку, которая движется по окружности с постоянной скоростью. Если мы будем следить за ее положением на вертикали, рассматривая его как функцию от времени, то получится синусоида.

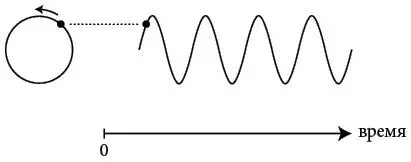
Поскольку окружности тесно связаны с циклами, синусоиды появляются везде, где есть циклические явления, – от смены времен года до колебаний камертона и частоты переменного тока в 50 Гц (герц), используемого в лампах и электрических сетях. Раздражающее гудение различных бытовых приборов, как правило, представляет собой звук с частотой 50 Гц (1 Гц = 1 колебание в секунду). Это надежный признак переменного тока, вырабатываемого электрогенераторами, крутящимися с такой частотой. Там, где есть круговое движение, есть и синусоиды.

Любая синусоида полностью определяется четырьмя основными характеристиками: периодом, средним значением, амплитудой и фазой.

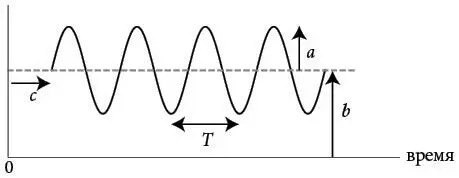
Эти четыре параметра истолковываются просто. Период T указывает, сколько времени требуется волне для прохождения одного полного цикла. Для рассматриваемых данных по продолжительности светового дня T составляет 365,25 дня (именно эта лишняя четверть дня – причина, по которой раз в четыре года нужен високосный год, чтобы поддерживать синхронизацию календаря с природными циклами). Среднее значение синусоиды b – это ее сдвиг по вертикали. Для нашего примера это типичное количество минут в световом дне в Нью-Йорке, усредненное по всем дням 2018 года. Амплитуда a волны говорит нам, сколько дополнительных минут света приходится на самый длинный день года по сравнению со средним днем. Наконец, фаза волны c сообщает день, когда волна на пути вверх пересекает свое среднее значение: это происходит около дня весеннего равноденствия.

Эти четыре параметра – a, b, c, T – можно представлять как четыре рукоятки, которые позволяют регулировать форму и положение синусоиды. Они действуют так: b -рукоятка перемещает синусоиду вверх и вниз; c -рукоятка двигает ее влево и вправо; T -рукоятка контролирует, как быстро волна колеблется, сжимая и растягивая ее по горизонтальной оси; и, наконец, a -рукоятка определяет, насколько сильный размах у колебаний.

Если бы мы могли каким-то образом настроить эти рукоятки так, чтобы синусоида проходила через все нарисованные нами ранее точки, то это позволило бы существенно сжать информацию и означало бы, что вместо 27 значений мы бы обошлись всего четырьмя параметрами такой подобранной синусоиды, то есть сжали бы данные в 27/4 = 6,75 раза. В реальности же, поскольку у нас один из параметров – год, по сути, мы можем играть всего с тремя параметрами, что дает нам сжатие в 27/3 = 9 раз. Такое уменьшение возможно, потому что наши данные не случайны. Они подчинены некоторой закономерности, а синусоида воплощает ее и делает за нас всю работу.

Единственная загвоздка – отсутствие синусоиды, которая бы идеально проходила через все точки. Этого следует ожидать при подгонке к реальным данным идеализированной модели: определенные расхождения неизбежны, но всегда есть надежда, что они окажутся незначительными. Для их минимизации требуется найти синусоиду, которая максимально близко подходит к нашим точкам. Вот тут-то в игру и вступает анализ.

На рисунке ниже показана наилучшая синусоида, определяемая алгоритмом оптимизации, который я объясню чуть ниже.

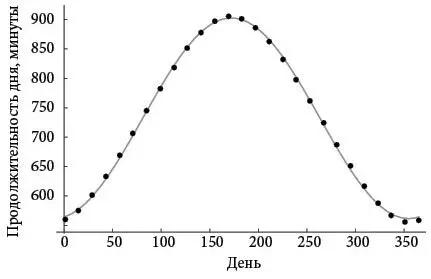
Но сначала обратите внимание, что результирующая кривая подходит не идеально. Например, она недостаточно низка в декабре, когда дни очень короткие и данные попадают ниже кривой. Тем не менее простая синусоида, безусловно, отражает суть происходящего. В зависимости от наших целей такое качество приближения может оказаться достаточным.

Но при чем тут анализ? Он помогает оптимально выбрать четыре параметра. Представьте, что вы поворачиваете эти четыре рукоятки, добиваясь наилучшей настройки, – нечто вроде поворота ручек на радиоприемнике для получения самого сильного сигнала. Фактически это то, что делал Ферма в задаче с багажной полкой, когда искал параметры самой вместительной коробки. Он менял единственный параметр x , длину боковой стороны коробки, и искал сигнал о максимальном объеме коробки. В нашем же случае требуется настроить четыре параметра. Однако основная идея та же. Мы должны добиться сигнала оптимальности, меняя четыре параметра.

Если подробнее, то работает это так. Мы вычисляем погрешность (иными словами, ошибку) для любого конкретного набора значений для четырех параметров, то есть разницу между соответствующей синусоидой и реальными данными во всех 27 точках года. Естественный критерий при выборе наилучшей кривой – чтобы общая ошибка по всем 27 точкам была настолько мала, насколько это возможно. Однако при этом общая ошибка – не самая удачная вещь, потому что нам не нужно, чтобы отрицательные ошибки компенсировали положительные и в результате складывалось ложное впечатление, что кривая подходит хорошо, хотя в реальности это не так. Отклонения вниз так же плохи, как и вверх, и от обоих нужно избавляться; нельзя допускать, чтобы они компенсировали друг друга. По этой причине математики рассматривают не ошибки, а квадраты ошибок. Такая мера отклонения будет всегда неотрицательной, и отклонения в разных точках не смогут при сложении аннулировать друг друга. (Это один из примеров практической пользы правила, что отрицательное число, умноженное на отрицательное, будет положительным. Квадрат отрицательной ошибки дает положительную меру погрешности, как нам и нужно.) Итак, основная идея при подборе четырех параметров синусоиды – минимизировать общую квадратичную ошибку для кривой. Этот подход называется методом наименьших квадратов и работает лучше всего, когда данные подчинены какой-то закономерности, как в нашем случае.