Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Однако Снелл обнаружил, что значение sin a / sin b зависит от материала двух сред. Воздух и вода давали одно постоянное соотношение, тогда как воздух и стекло – другое. Он понятия не имел, почему работает этот закон синусов. Он просто работал. Это был просто голый факт о свете.

Декарт повторно открыл закон синусов Снелла [174]и опубликовал его в своем труде 1637 года «Диоптрика», не подозревая, что как минимум три человека уже установили его раньше: Снелл в 1621 году, английский астроном Томас Хэрриот в 1602-м и персидский математик Абу Сад ал-Ала ибн Сахль еще в 984-м.

Декарт дал механическое объяснение закону синусов, в котором (ошибочно) предположил, что свет движется быстрее в более плотной среде. С точки зрения Ферма, это звучало странно и противоречило здравому смыслу. Пытаясь быть полезным и будучи наивным и простодушным человеком, тулузский провинциал изложил свои мягкие критические замечания по поводу теории Декарта и отправил их парижским математикам, которые поинтересовались его мнением.

Ферма не знал, что эти люди были заклятыми врагами Декарта и использовали провинциального ученого для своих целей. И, как мог бы предвидеть даже ребенок, когда Декарт узнал о комментариях Ферма, он решил, что на него нападают. Он никогда не слышал об этом юристе из Тулузы. Для него Ферма был малоизвестным любителем-провинциалом, человеком, от которого можно легко отмахнуться, как от назойливого комара. В течение нескольких следующих лет Декарт относился к Ферма снисходительно и заявлял, что тот случайно натолкнулся на его результаты.

Однако перенесемся на двадцать лет вперед. В 1657 году, уже после смерти Декарта, врач и философ Марен Кюро де ла Шамбр попросил Ферма вернуться к старому вопросу о преломлении. Просьба Кюро побудила Ферма внимательно рассмотреть эту задачу, используя свои знания об оптимизации.

Ферма догадывался, что свет использует оптимальность. А точнее, он предположил, что свет всегда следует по пути наименьшего сопротивления между любыми двумя точками, что, по его мнению, означало, что он двигается по самому быстрому маршруту. Такой принцип наименьшего времени [175]объяснял, почему свет движется по прямой в однородной среде и почему при отражении от зеркала угол падения равен углу отражения. Но мог ли принцип наименьшего времени также верно объяснить, почему луч меняет направление при переходе из одной среды в другую? Мог ли он объяснить закон преломления?

Ферма не был в этом уверен. Такие вычисления не из легких. От источника в одной среде к целевой точке в другой свет может двигаться бесконечным числом прямолинейных путей, каждый из которых изгибается на границе двух сред по-своему.

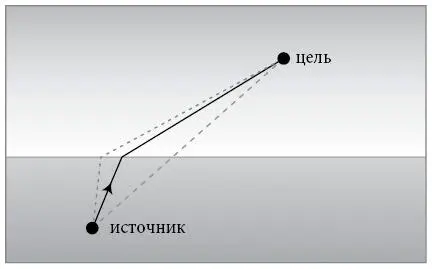
Вычислить минимум среди всех этих времен перемещения было сложно, в особенности на стадии зарождения дифференциального исчисления. У Ферма не было никаких инструментов, кроме старого метода двойного пересечения. К тому же он боялся получить неправильный ответ. Как он написал Кюро, «страх обнаружить после долгих и трудных вычислений какое-то неправильное и фантастическое соотношение, а также моя природная леность оставили этот вопрос в том же состоянии» [176].

Понадобилось пять лет, в течение которых Ферма работал над другими задачами, чтобы любопытство все же взяло верх. В 1662 году он заставил себя произвести нужные вычисления. Это было изнурительно и неприятно. Но, пробираясь сквозь заросли символов, он начал кое-что замечать. Слагаемые стали сокращаться. Алгебра работала. И вот он: закон синусов. В письме Кюро Ферма назвал эти вычисления «самыми необычными, самыми непредвиденными и самыми счастливыми» из всех, что он когда-либо делал. «Я был так удивлен этому неожиданному событию, что едва могу оправиться от изумления» [177].

Ферма применил свою зачаточную версию дифференциального исчисления к физике. До него этого никто не делал. Тем самым он показал, что свет двигается наиболее эффективным способом – не самым прямым путем, а самым быстрым. У света множество возможных путей, но он каким-то образом знает (или ведет себя так, словно знает), как добраться из одной точки в другую максимально быстро. Это стало важной подсказкой к тому, что анализ как-то встроен в операционную систему Вселенной.

Позже принцип наименьшего времени был обобщен до принципа наименьшего действия [178], где термин «действие» имеет технический смысл, в который нам сейчас незачем вдаваться. Было установлено: такой принцип оптимизации, согласно которому природа ведет себя наиболее экономным способом в каком-то точно определенном смысле, верно предсказывает законы механики. В XX веке принцип наименьшего действия был распространен на общую теорию относительности, квантовую механику и другие области современной физики. Он даже произвел сильное впечатление на философию XVII века, когда Готфрид Вильгельм Лейбниц сказал свою знаменитую фразу «Все к лучшему в этом лучшем из миров», и эта оптимистическая точка зрения была позднее спародирована Вольтером в «Кандиде». Идея использования принципа оптимальности для объяснения физических явлений и вывода следствий с помощью анализа зародилась именно с этого вычисления Ферма.

Технические методы оптимизации Ферма также позволяли ему находить касательные к кривым. Эта задача по-настоящему приводила Декарта в бешенство.

Слово «касательная» происходит от глагола «касаться». Эта прямая не пересекает кривую в двух точках, а соприкасается с нею в одной точке.

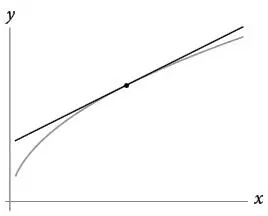
Условия касания аналогичны условиям максимума или минимума. Если мы берем прямую и пересекаем ею кривую, а затем начинаем непрерывно двигать прямую вверх или вниз, то касание возникает, когда две точки пересечения сливаются в одну.

Где-то в конце 1620-х годов Ферма научился находить касательные практически для всех алгебраических кривых (это означает, что кривая выражается многочленом различных степеней x и y ; функции, не являющиеся алгебраическими, называются трансцендентными – это синусы, логарифмы и так далее). Благодаря своей идее двойного пересечения он мог вычислить все, что мы делаем сегодня с помощью производных.

У Декарта был собственный метод нахождения касательных [179]. В «Геометрии» 1637 года он с гордостью объявил о нем миру. Не подозревая, что Ферма уже решил эту задачу, Декарт независимо пришел к идее двойного пересечения, но для пересечения кривых использовал не прямые, а окружности. Вблизи точки касания типичная окружность либо пересекает кривую в двух точках, либо не пересекает вообще.