Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Основные векторные и матричные операции:

• dotprod(U,V) — возвращает скалярное произведение векторов U и V;

• crossprod(U,V) — возвращает векторное произведение векторов U и V;

• norm(V) или norm(M) — возвращает норму вектора или матрицы;

• copyinto(A,B,i,j) — копирует матрицу А в В для элементов последовательно от i до j;

• concat(M1,M2) — возвращает объединенную матрицу с горизонтальным слиянием матриц М1 и М2;

• stack(M1,M2) — возвращает объединенную матрицу с вертикальным слиянием М1 и М2;

• matadd(A,B) и evalm(A+B) — возвращает сумму матриц А и В;

• multiply(A,B) и evalm(A&*B) — возвращает произведение матриц А и В;

• adjoint(M) или adj(M) — возвращает присоединенную матрицу, такую, что M∙adj(M) дает диагональную матрицу, определитель которой есть det(M);

• charpoly(M,lambda) — возвращает характеристический полином матрицы М относительно заданной переменной lambda;

• det(M) — возвращает детерминант (определитель) матрицы М;

• Eigenvals(M,vector) — инертная форма функции, возвращающей собственные значения матрицы М и (при указании необязательного параметра vector) соответствующие им собственные векторы;

• jordan(M) — возвращает матрицу М в форме Жордана;

• hermite(M) — возвращает матрицу М в эрмитовой форме;

• trace(M) — возвращает след матрицы М;

• rank(M) — возвращает ранг матрицы М;

• transpose(M) — возвращает транспонированную матрицу М;

• inverse(M) или evalm(1/M) — возвращает матрицу, обратную к М;

• singularvals(A) — возвращает сингулярные значения массива или матрицы А.

Приведем примеры применения некоторых из этих функций (файл linalgop):

> M:=matrix(2,2, [a,b,с,d]);

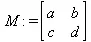
> transpose(M);

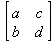
> inverse(M);

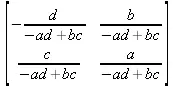
> det(M);

> rank(M);

> trace(M);

> M:=matrix(2,2,[1,2,3,4]);

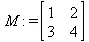
> ev:=evalf(Eigenvals(M,V));

> eval(V);

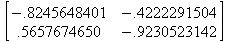
> charpoly(M,p);

> jordan(M);

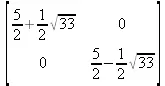
> A:= array([[1,0,1],[1,0,1],[0,1,0]]);

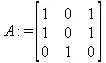
> singularvals(А);

В приведенных примерах полезно обратить внимание на то, что многие матричные функции способны выдавать результаты вычислений в аналитическом виде, что облегчает разбор выполняемых ими операций.

Одной из самых распространенных задач линейной алгебры является решение систем линейных уравнений. Ниже представлен простой пример составления и решения трех систем линейных уравнений с применением функций, входящих в пакет linalg (файл sle):

> with(linalg):

> C:=matrix(3,3,[[4,8,2],[6,2,3],[3,7,11]]);

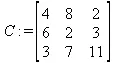
> B:=matrix(3,1, [5,6,1]);

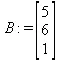
> A:=evalm(C);

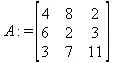
> A1 :=copyinto(В, С, 1, 1);

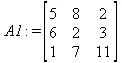
> C:=evalm(A):А2:=copyinto(В,С,1,2);

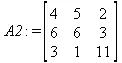
> C:=evalm(A):A3:=copyinto(В,С,1,3);

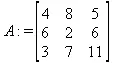
> x1:=det(A1)/det(А);

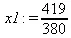
> x2:=det(A2)/det(A);

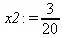
> x3:=det(A3)/det(a);

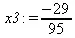
А теперь рассмотрим пример решения матричного уравнения в символьном виде:

> A:=matrix(2,2,[a,b,с,d]);

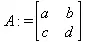
> В:=vector(2, [с,d]);

> X:=linsolve(А,В);

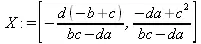
Следующий пример показывает решение более сложной системы линейных уравнений с комплексными коэффициентами:

> А:=matrix(2,2,[[10+200*1,-200*1],[-200*1,170*1]]);

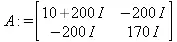
> B:=vector(2, [5,0]);

> X:=multiply(inverse(А),В);

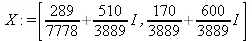
> Digits:=5: convert(eval(X),float);

На этот раз решение получено использованием функций умножения матриц и вычисления обратной матрицы в виде X=А -1∙В, то есть в матричном виде. В конце примера показано преобразование результатов с целью их получения в обычной форме комплексных чисел с частями, представленными в форме чисел с плавающей точкой.

Как видно из описанного, многие вычисления имеют результаты, представляемые в форме матриц. Иногда такие результаты можно наглядно представить графически, например, в виде гистограммы. Она представляет собой множество столбцов квадратного сечения, расположенных на плоскости, образованной осями строк (row) и столбцов (column) матрицы. При этом высота столбцов определяется содержимым ячеек матрицы.

Такое построение обеспечивает графическая функция matnxplot из пакета plots. На рис. 5.1 показано совместное применение этой функции с двумя функциями пакета linafg, формирующими две специальные матрицы Аи В.

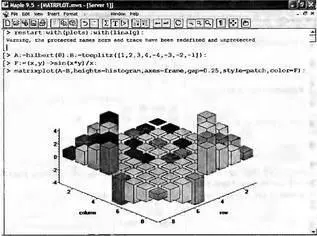
Рис. 6.1. Графическое представление матрицы