Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

• frobenius — вычисляет форму Фробениуса (Frobenius) матрицы;

• gausselim — Гауссово исключение в матрице;

• gaussjord — синоним для rref (метод исключения Гаусса-Жордана);

• geneqns — генерирует элементы матрицы из уравнений;

• genmatrix — генерирует матрицу из коэффициентов уравнений;

• grad — градиент векторного выражения;

• GramSchmidt — вычисляет ортогональные векторы;

• hadamard — вычисляет ограничение на коэффициенты детерминанта;

• hessian — вычисляет гессиан-матрицу выражения;

• hilbert — создает матрицу Гильберта;

• htranspose — находит эрмитову транспонированную матрицу;

• ihermite — целочисленная эрмитова нормальная форма;

• indexfunc — определяет функцию индексации массива;

• innerprod — вычисляет векторное произведение;

• intbasis — определяет базис пересечения пространств;

• ismith — целочисленная нормальная форма Шмитта;

• iszero — проверяет является ли матрица ноль-матрицей;

• jacobian — вычисляет якобиан векторной функции;

• JordanBlock — возвращает блок-матрицу Жордана;

• kernel — находит базис ядра преобразования, соответствующего данной матрице;

• laplacian — вычисляет лапласиан;

• leastsqrs — решение уравнений по методу наименьших квадратов;

• linsolve — решение линейных уравнений;

• Ludecomp — осуществляет LU-разложение;

• minpoly — вычисляет минимальный полином матрицы;

• mulcol — умножает столбец матрицы на заданное выражение;

• mulrow — умножает строку матрицы на заданное выражение;

• multiply — перемножение матриц или матрицы и вектора;

• normalize — нормализация вектора;

• orthog — тест на ортогональность матрицы;

• permanent — вычисляет перманент матрицы — определитель, вычисляемый без перестановок;

• pivot — вращение относительно элементов матрицы;

• potential — вычисляет потенциал векторного поля;

• Qrdecomp — осуществляет QR-разложение;

• randmatrix — генерирует случайные матрицы;

• randvector — генерирует случайные векторы;

• ratform — вычисляет рациональную каноническую форму;

• references — выводит список основополагающих работ по линейной алгебре;

• rowspace — вычисляет базис пространства строки;

• rowspan — вычисляет векторы охвата для места столбца;

• rref — реализует преобразование Гаусса-Жордана матрицы;

• scalarmul — умножение матрицы или вектора на заданное выражение;

• singval — вычисляет сингулярное значение квадратной матрицы;

• singularvals — возвращает список сингулярных значений квадратной матрицы;

• smith — вычисляет Шмиттову нормальную форму матрицы;

• submatrix — извлекает указанную подматрицу из матрицы;

• subvector — извлекает указанный вектор из матрицы;

• sumbasis — определяет базис объединения системы векторов;

• swapcol — меняет местами два столбца в матрице;

• swaprow — меняет местами две строки в матрице;

• sylvester — создает матрицу Сильвестра из двух полиномов;

• toeplitz — создает матрицу Теплица;

• trace — возвращает след матрицы;

• vandermonde — создает вандермондову матрицу;

• vecpotent — вычисляет векторный потенциал;

• vectdim — определяет размерность вектора;

• wronskian — вронскиан векторных функций.

Назначение многих функция вполне очевидно из названия. Далее мы рассмотрим более подробно некоторые функции из этого пакета. С деталями синтаксиса (достаточно разнообразного) для каждой из указанных функций можно ознакомиться в справочной системе Maple. Для этого достаточно использовать команду ?name;, где name — имя функции (из приведенного списка).

Для интерактивного ввода матриц можно, определив размерность некоторого массива, использовать функцию entermatrix:

> с A:=array(1..3,1..3);

После исполнения этого фрагмента документа диалог с пользователем имеет следующий вид:

> entermatrix(А);

enter element 1,1 > 1;

enter element 1,2 > 2;

enter element 1,3 > 3;

enter element 2,1 > 4;

enter element 2,2 > 5;

enter element 2,3 > 6;

enter element 3,1 > 7;

enter element 3,2 > 8;

enter element 3,3 > 9;

> В:=(%);

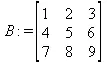
> В[1,1];

> В[2,2];

> В[3,3];

В библиотечном файле linalg имеются следующие функции для задания векторов и матриц:

• vector(n,list) — создание вектора с n элементами, заданными в списке list;

• matrix(n,m,list) — создание матрицы с числом строк n и столбцов m с элементами, заданными списком list.

Ниже показано применение этих функций (файл linalgop):

> V:=vector(3, [12, 34, 56]);

> M:=matrix(2,3, [1,2,3,4]);

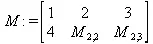
> V[2];

> М[1, 3];

> М[2, 3];

Обратите внимание на последние примеры — они показывают вызов индексированных переменных вектора и матрицы.

Для работы с векторами и матрицами Maple имеет множество функций, входящих в пакет linalg. Ограничимся приведением краткого описания наиболее распространенных функций этой категории.

Операции со структурой отдельного вектора Vи матрицы М:

• coldim(M) — возвращает число столбцов матрицы М;

• rowdim(M) — возвращает число строк матрицы М;

• vectdim(V) — возвращает размер вектора V;

• col(M.i) — возвращает i-й столбец матрицы М;

• row(M,i) — возвращает i-ю строку матрицы М;

• minor(M,i,j) — возвращает минор матрицы М для элемента с индексами i и j;

• delcols(M,i..j) — удаляет столбцы матрицы М от i-го до j-го;

• delrows(V,i..j) — удаляет строки матрицы М от i-й до j-й;

• extend(M,m,n,x) — расширяет матрицу М на m строк и n столбцов с применением заполнителя х.