Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Квадратная матрица — матрица, у которой число строк m равно числу столбцов n. Пример квадратной матрицы размера 3×3:

Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением n элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:

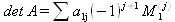
где M 1 — определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием первой строки и j- го столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.

Сингулярная (вырожденная ) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.

Единичная матрица — это квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размера 4×4:

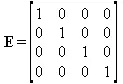
Сингулярные значения матрицы А — квадратные корни из собственных значений матрицы transpose(A)∙А, где transpose(A) — транспонированная матрица А (см. ее определение ниже).

Транспонированная матрица — матрица, у которой столбцы и строки меняются местами, то есть элементы транспонированной матрицы удовлетворяют условию A T(i,j)=A(j,i). Приведем простой пример.

Исходная матрица:

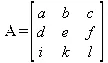
Транспонированная матрица:

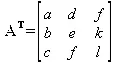
Обратная матрица — это матрица М -1 , которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.

Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.

Диагональ матрицы — расположенные диагонально элементы А i,iматрицы А. В приведенной ниже матрице элементы диагонали представлены заглавными буквами:

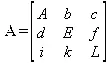
Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия поддиагоналей (элементы d и k ) и наддиагоналей (элементы b и f ). Матрица, все элементы которой, расположенные кроме как на диагонали, поддиагонали и наддиагонали, равны нулю, называется ленточной.

Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы.

След матрицы — сумма диагональных элементов матрицы.

Матрица в целой степени — квадратная матрица в степени n ( n — целое неотрицательное число), определяемая следующим образом: М 0 = Е, М 1 = М, М 2 =ММ,…, М n = М n-1 М.

Идемпотентная матрица — матрица, отвечающая условию Р²= Р.

Симметрическая матрица — матрица, отвечающая условию А т = А.

Кососимметрическая матрица — матрица, отвечающая условию А т =- А.

Ортогональная матрица — матрица, отвечающая условию А т = А -1 .

Нуль-матрица — матрица, все элементы которой равны 0.

Блок-матрица — матрица, составленная из меньших по размеру матриц, также можно представить как матрицу, каждый элемент которой — матрица. Частным случаем является блок-диагональная матрица — блок-матрица, элементы-матрицы которой вне диагонали — нуль-матрицы.

Комплексно-сопряженная матрица — матрица Ā, полученная из исходной матрицы Азаменой ее элементов на комплексно-сопряженные.

Эрмитова матрица — матрица А, удовлетворяющая условию Ā= А т .

Собственный вектор квадратной матрицы А— любой вектор х∈ V n , х≠0, удовлетворяющий уравнению Ах=γ х, где γ — некоторое число, называемое собственным значением матрицы А.

Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена — | А-γ Е|.

Собственные значения матрицы — корни ее характеристического многочлена.

Норма — обобщенное понятие абсолютной величины числа.

Норма трехмерного вектора ||х||— его длина.

Норма матрицы — значение sup( ||Ax||/||x||).

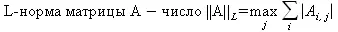
Матричная форма записи системы линейных уравнений — выражение А∙Х= В, где А— матрица коэффициентов системы, X— вектор неизвестных и В— вектор свободных членов. Один из способов решения такой системы очевиден — X= А -1∙В, где А -1 — обратная матрица.

Как известно, обычная система линейных уравнений имеет вид:

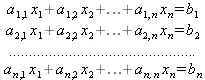
Здесь а 1,1, а 1,2, …, a n,n — коэффициенты, образующие матрицу Аи могущие иметь действительные или комплексные значения, х 1, х 2, …, х n — неизвестные, образующие вектор Xи b 1, b 2, …, b n— свободные члены (действительные или комплексные), образующие вектор В. Эта система может быть представлена в матричном виде как АХ=В, где А— матрица коэффициентов уравнений, X— искомый вектор неизвестных и В— вектор свободных членов. Из такого представления системы линейных уравнений вытекают различные способы ее решения: X= В/А(с применением матричного деления), X= А -1 В(с инвертированием матрицы А) и так далее.