Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> 101!;

> (101!+1)-101!;

> (10005!)/10000!;

> 2^101-2^100;

> 2^(2^(2^2));

> 2^101-2^100.0;

> Digits;

Обратите внимание на то, что в последнем примере точность резко потеряна, так как показатель степени 100.0 был задан как число с плавающей точкой. Соответственно и результат оказался в форме такого числа. Число верных цифр результата задает системная переменная Digits (по умолчанию 10).

Приведем еще пару примеров точных вычислений некоторых функций (с точностью до 150 знаков мантиссы):

> evalf(ехр(1),150);

> evalf(sin(1.),150);

Разработчики систем Maple и Mathematica утверждают, что в принципе возможны вычисления и с плавающей точкой с заданием до миллиона точных цифр мантиссы. Практически такая точность почти никогда не нужна, по крайней мере для физиков и инженеров. Например, всего 39 точных цифр числа π достаточно, чтобы вычислить длину окружности всей Вселенной с точностью до диаметра атома водорода. Однако истинные математики одно время были просто «помешаны» на вычислении числа π с большой точностью. Кое кто потратил на это всю жизнь. Выдающийся вклад в такие расчеты внес Рамануджан, который еще в 1916 году предложил алгоритмы и формулы для вычисления числа π с произвольной точностью.

На рис. 2.1 представлено задание одной из самых известных формул Рамануджана. Уже первый член суммы этой формулы (k= 1) дает значение числа π с погрешностью вычисления менее 3∙10 -8. Увеличение k на 1 каждый раз увеличивает число верных десятичных знаков на 8, т. е. в сто миллионов раз! В принципе эта формула может дать до миллиарда и более точных знаков числа π!

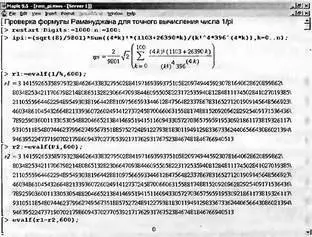
Рис. 2.1. Проверка вычислений по формуле Рамануджана

У инженеров формула Рамануджана может вызвать приступ головной или зубной боли. Уж больно несуразна она с первого взгляда. О какой точности можно говорить, если на подавляющем большинстве языков программирования корень квадратный из двух, факториал и степень вычисляются всего с 8–15 точными знаками?

Но, системы Maple 9.5, благодаря встроенному аппарату точной арифметики, способна обеспечить эффективную проверку подобных формул. В нашем случае мы ограничились случаем n= 100 (максимальное значение k) и провели вычисления «всего» 600 цифр числа π — с тем, чтобы результаты вместились в один рисунок. И они говорит сам за себя — все цифры при вычислении числа π по формуле Рамануджана и по встроенному в Maple алгоритму полностью совпали, а вычисленная ошибка равна нулю!

Maple, естественно, как и другие СКМ, может работать с комплексными числами вида z=Re(z)+I∙Im(z). Мнимая единица в комплексном числе (корень квадратный из -1) обозначается как I. Функции Re(z) и Im(z) возвращают действительную и мнимую части комплексных чисел. На комплексной плоскости числа задаются координатами точек (х, у) — рис. 2.2.

Рис. 2.2. Представление обычных и комплексных чисел на плоскости

Для представления чисел на рис. 2.2 используется функция pointplot(list), где list — список координат точек. Эта функция становится доступной при подключении пакета plots командой with(plots). Кроме того, использована функция вывода ряда графических объектов на один график — display (см. далее описание представления комплексных чисел).

Примеры задания комплексного числа и вывода его действительной и мнимой частей представлены ниже:

> a+b*I;

> 1.25+Pi*I;

> Re(1.25+Pi*I);

> Im(1.25+Pi*I);

Комплексные числа обычно представляют на так называемой комплексной плоскости, у точек которой координата x задает действительную часть комплексного числа, а у (мнимая ось) показывает мнимую часть такого числа. На рис. 2.2 показано задание в виде радиус-векторов комплексного числа z=4+3I, -z и комплексно-сопряженного числа 4-3I. А на рис. 2.3 показан пример вычисления корней уравнения z^n=1 для случая n=16 (другие случаи читатель может рассмотреть самостоятельно, просто изменив n). Нетрудно заметить, что корни уравнения — комплексные числа и что на комплексной плоскости они ложатся на окружность единичного радиуса.

Рис. 2.3. Вычисление корней уравнения z^n=1 и расположение корней на комплексной плоскости

Окружность радиуса 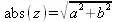представляет абсолютное значение комплексного числа z=a+b *I. Она является геометрическим множеством комплексных чисел, образованных концом вращающегося радиус-вектора числа z вокруг его начала в точке (0, 0) комплексной плоскости, иллюстрацией чего и является частный пример рис. 2.2. Позже мы рассмотрим ряд функций для работы с комплексными числами.

Числа могут служить объектами ввода, вывода и константами, входящими в математические выражения. Функция type(x, numeric) позволяет выяснить, является ли х числом. Если является, то она возвращает логическое значение true (истина), а если нет, то false (ложь). Например:

> type(2,numeric);

> type(2.6,numeric);

> type(Pi,numeric);

> type(I,numeric);

> type(3/7,numeric);

> type(3^7,numeric);

> type(х^2,numeric);

Функции type(x, integer), type(x, rational) и type(x, fraction) можно использовать для проверки того, имеет ли х значение, соответственно, целого числа, рационального числа или простой дроби:

> type(123,integer);

> type(123.,integer);

> type(123/456,rational);

> type(1./3,rational);

> type(1/2,fraction);

> type(0.5,fraction);