Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

В Maple возможна работа с числами, имеющими различное основание (base), в частности, с двоичными числами (основание 2 — binary), восьмеричными (основание 8 — octal) и шестнадцатиричными (основание 16 — hex). Функция convert позволяет легко преобразовывать форматы чисел:

> convert(12345,binary);

> convert(%,decimal,binary);

> convert(12345,octal);

> convert(123456,hex);

> convert(%,decimal,hex);

Помимо приведенных вариантов функция convert имеет еще ряд других форм. С ними можно познакомиться с помощью справки по этой мощной функции. В дальнейшем будет приведен ряд других применений этой функции.

В целом ряде случаев работа вычислителей Maple по умолчанию в области комплексных значений данных нежелательна, поскольку приводит к представлению результатов также в комплексном виде:

> restart:simplify(sqrt(х^2)); ln(-2); solve(х^3-8=0,x);

В связи с этим в Maple введен новый математический пакет расширения RealDomain, переводящий вычисления в область реальных значений данных. Вызов пакета обеспечивается следующим образом:

> restart:with(RealDomain);

Нетрудно заметить, что этот пакет переопределяет элементарные функции и некоторые другие вычислительные функции таким образом, что вычисления с ними ведутся только с реальными (вещественными, действительными) числами. Это видно из представленных ниже примеров:

> simplify(sqrt(х^2));

> ln(-2);

> solve(х^3-8=0,х);

Следует отметить, что вычисляемые выражения при работе с данным пакетом надо размещать после его загрузки.

В старых версиях Maple функция plot нередко отказывалась строить графики функций, значения которых были комплексными числами. Но уже в Maple 8 алгоритм построения графиков переработан. Теперь, если выражение, по которому строится график, в ходе оценивания дает мнимую часть, она отбрасывается, так что строится график только действительной части выражения. Малые по модулю мнимые части также нередко отбрасываются — впрочем, когда именно не совсем ясно.

Рис. 2.4 дает примеры этого. В верхней части документа строятся графики функции квадратного корня от х, логарифма и синуса. Нетрудно заметить, что для квадратного корня и логарифма строится и впрямь только та часть графиков, где значения функций действительны — при х положительном. Для х< 0 строится только график функции синуса, поскольку синус дает вещественные значения при любом x — как положительном, так и отрицательном.

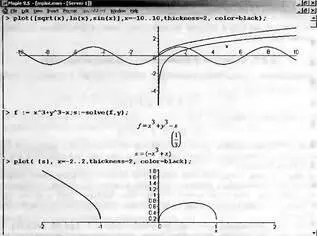
Рис. 2.4. Особые случаи применения функции plot

Еще более интересен случай, представленный снизу рис. 2.4. Здесь функция задана как решение выражения f, которое дает корни в виде комплексных выражений. Несмотря на это возможные части графика функции f(x) строятся.

Сложными являются такие типы данных, которые являются представлением множественных и подчас разнохарактерных объектов. Нередко такие данные включают как часть себя рассмотренные выше простые типы данных.

В системе Maple любые выражения могут включаться в наборы , относящиеся к множественным данным. Такие наборы в виде множеств создаются с помощью фигурных скобок { }:

> {a,b,a,a,b,d,e,c,d};

> {10,2+3,4+4,8,5,1};

> {`Hello` ,`my`,`friend`};

Отличительная черта множеств — автоматическое устранение из них повторяющихся по значению элементов. Кроме того, Maple расставляет элементы множеств в определенном порядке — числа в порядке увеличения значения, а символы и строки в алфавитном порядке. Для множеств нет строгого математического определения, и мы будем считать их наборами, удовлетворяющими перечисленным выше признакам.

Для создания упорядоченных наборов — списков — служат квадратные скобки []:

> [10,2+3,4+4,8,5,1];

> [а, b, c, a, a, d, d, e] ;

Как нетрудно заметить, элементы списков преобразуются и выводятся строго в том порядке, в каком они были заданы. Списки широко применяются для задания векторов и матриц.

В ряде случаев, например, при подготовке данных для двумерных графиков, возникает необходимость в подготовке парных списков — скажем, координат точек ( х, у) графика. Для этого можно использовать функцию zip(f, u, v) или zip(f, u, v, d). Здесь f — бинарная функция, u, v — списки или векторы, d — необязательное значение.

Примеры применения функции zip даны на рис. 2.5. Там же показано применение этих средств для построения точек, представляющих множество действительных чисел на плоскости. Для этого использована функция pointplot из пакета plots.

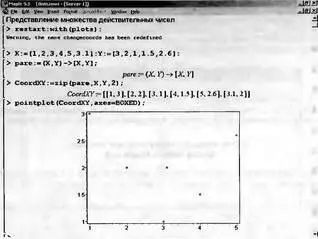
Рис. 2.5. Представление множества чисел на плоскости

Важным типом данных являются списки или листы. В Maple 9.5 они создаются с помощью квадратных скобок, например:

[1,2,3,4] — список из четырех целых чисел;

[1,2.34,5] — список из двух вещественных и одного целого числа;

[a,b, "Привет"] — список из двух символов (переменных) и строковой константы;

[sin(x), 2*cos(x),a^2-b] — список из трех математических выражений.

Для создания векторов (одномерных массивов) и матриц (двумерных массивов) служит функция array. Обычно она используется в следующих формах:

array[a..b,s1] — возвращает вектор с индексами от а до b и значениями в одномерном списке s1;

array[a..b,c..d,s2] — возвращает матрицу с номерами строк от а до b, номерами столбцов от с до d и значениями в двумерном списке s2.

Примеры задания вектора и матрицы представлены ниже:

array(1..3,[х,у,х+у]) — создает вектор с элементами x, у и х+y;

array(1..2,1..2,[[a,b],[c,d]]) — квадратная матрица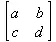

Для создания векторов может использоваться также конструктор векторов Vector[o](d, init, ro, sh, st, dt, f, а, о) с рядом опционально заданных параметров. В этой книге эта конструкция практически не используется. Векторы и матрицы можно также задавать с помощью угловых скобок: