Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Продолжим изучение данного «каверзного» интеграла. Опробуем силы Maple на интеграле более общего вида, где конкретный показатель степени заменен на обобщенный — n. Здесь нас ожидает приятный сюрприз — Maple с легкостью выдает аналитическое решение для данного определенного интеграла:

> у:=(n)->int(х^n*ехр(-х),х=0..1);

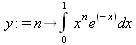
> y(n);

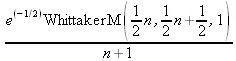
> y(20);

> evalf(%,30);

> у(20.);

Однако радоваться несколько преждевременно. Многие ли знают, что это за специальная функция — WhittakerM? Но хуже другое — Maple при конкретном n=20 дает грубо неверное решение — 0 (почему — уже объяснялось). Забавно, что при этом сама по себе функция WhittakerM вычисляется для n=20 без проблем:

> WhittakerM(10,10.5,1);

А теперь присмотритесь к новому результату вычисления злополучного интеграла. Оказывается, он уже не содержит больших чисел, свойственных прямому решению! Зная значение WhittakerM с погрешностью по умолчанию, можно уверенно вычислить приближенное численное значение интеграла с той же погрешностью, уже не прибегая к арифметике высокой точности:

> (ехр(-.5)*WhittakerM(10,10.5,1))/21;

На рис. 4.3 приведен график зависимости значений данного интеграла от показателя степени n при его изменении от 0 до 50. Плавный ход графика показывает, что в вычислении данного интеграла нет никаких признаков неустойчивости решения при изменении n, если соблюдать правило выбора достаточно малой погрешности вычислений.

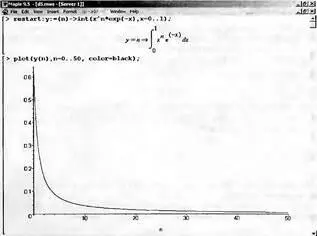
Рис. 4.3. Значение интеграла от х^nехр(-х) как функция n

Наличие у функции особых (сингулярных) точек нередко затрудняет выполнение с ней ряда операций, таких как численное интегрирование. В этом случае могут помочь соответствующие параметры. Например, вычисление в Maple 8/9 следующего интеграла дает явно неудобное выражение в виде набора значений, разных для разных интервалов изменения a:

> int(1/(х+а)^2,х=0..2);

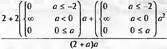
Этот интеграл расходится, поскольку при x=-a подынтегральная функция устремляется в бесконечность, что и показывает приведенное выражение. График зависимости значения интеграла от параметра а имеет подозрительный вид.

Это как раз тот случай, когда надо обратить особое внимание на результаты полученные системой Maple. А теперь покажем, как выглядит этот пример при его решении в системе Maple 9.5 — рис. 4.4. Обратите внимание на «провал» графика в средней части.

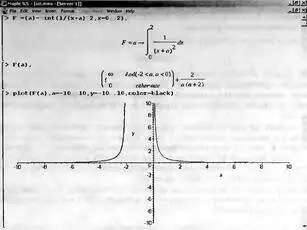
Рис. 4.4. Построение графика зависимости значений интеграла с подынтегральной функцией 1/(х+а)^2 от параметра a

Интересно, что если в нашем случае, применить параметр continuous (в апострофах) при вычислении интеграла, можно получить более простое выражение:

> int(1/(х+а)^2,х=0..2,`continuous`);

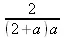
Рис. 4.5 показывает это решение с двумя важными дополнениями — оно представляется функцией пользователя, а ее график строится при изменении а от -10 до 10. «Провал» в средней части графика уже отсутствует.

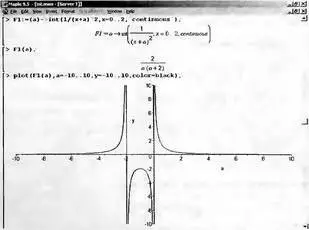
Рис. 4.5. Зависимость значения интеграла с подынтегральной функцией 1/(х+а)^2 и пределами от 0 до 2 от параметра а

Приведем еще один пример «каверзного» интеграла довольно простого вида:

> int(1/х^3,х=-1..2);

Этот интеграл не берется вообще, так что Maple совершенно справедливо об этом и сообщает. Но введение параметра CauchyPrincipalValue позволяет получить численное значение интеграла:

> int(1/х^3,х=-1..2,`CauchyPrincipalValue`);

Возьмем еще один наглядный пример — вычисление интеграла от синусоидальной функции при произвольно больших пределах, но кратных 2π! Очевидно, что при этом (учитывая равность площадей положительной и отрицательной полуволн синусоиды) значение интеграла будет равно 0. Например:

> int(sin(х),x=-1000*pi..1000*pi);

Однако распространение этого правила на бесконечные пределы интегрирования является грубейшей ошибкой. Интеграл такого рода уже не сходится и Maple дает соответствующий результат:

> int(sin(х),x=-infinity..infinity);

Во многих областях техники часто употребляются математически неточные выражения «затухающая синусоида» или «нарастающая синусоида». Возьмем, к примеру, широко распространенную функцию: у(t)=exp(-t)sin(2π). Построим ее график и вычислим определенный интеграл от этой функции с пределами от 0 до ∞ (рис. 4.6).

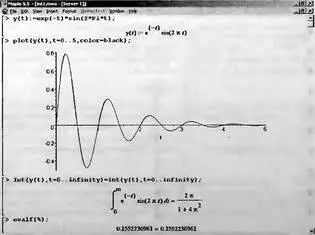
Рис. 4.6. График «затухающей синусоиды» и интеграл от нее с пределами от 0 до ∞

С первого взгляда на график видно, что каждая положительная полуволна функции (затухающей «синусоиды») явно больше последующей отрицательной полуволны. К тому же осцилляции функции быстро затухают и через десяток-другой периодов значение функции становится исчезающе малым. Вот почему Maple уверенно вычисляет интеграл с такой подынтегральной функцией. Ее свойство — неопределенность при t →∞ просто исчезает.

А теперь возьмем антипод этой функции — «синусоиду с экспоненциально нарастающей до стационарного значения 1 амплитудой». Такая функция записывается следующим образом:

Ее график и попытки вычисления интеграла с такой подынтегральной функцией приведены на рис. 4.7.

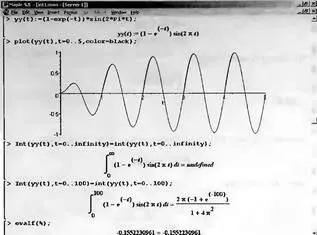
Рис. 4.7. График «экспоненциально нарастающей синусоиды» и интеграл от нее с пределами от 0 до ∞

Обратите внимание на то, что здесь прямое вычисление интеграла к успеху не привело, хотя из графика функции видно, что каждая положительная полуволна в близкой к t=0 области явно больше по амплитуде, чем последующая отрицательная полуволна. Однако, в отличие от предыдущей функции, при больших значениях аргумента данная функция вырождается в обычную синусоиду с неизменной (и равной 1) амплитудой. Вот почему Maple честно отказывается вычислять не сходящийся интеграл от такой «коварной» функции.