Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> Int(1/(t^2*(sqrt(t^2-9))), t=3..x) = int(1/(t^2*(sqrt(t^2-9))), t=3..x);

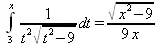
Увы, Maple 9.5 вычислять данный интеграл не желает — он его просто повторяет. Но, и в Maple 8 и в Maple 9.5 нужное значение определяется пределом этого выражения при х, стремящемся к бесконечности:

> Int(1/(x^2*(sqrt(х^2-9))),х=0..infinity) = value(Limit(rhs(%),x=infinity));

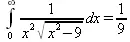
Этот пример наглядно показывает, что иногда полезны аналитические преобразования, выполняемые «вручную», то бишь с помощью своей головы. К сожалению, с подобными «фокусами» иногда приходится встречаться.

Приведенные примеры говорят о том, что и новые реализации Maple не лишены отдельных недостатков, возможно и привнесенных в их доработанное ядро. В общем, как говорят у нас в армии «Доверяй, но — проверяй!». Интегралы, представляемые через специальные математические функции, Maple 9.5/10 нередко вычисляет хуже, чем система Mathematica 4.5/5.

К интересному классу интегралов относятся определенные интегралы с переменными пределами интегрирования. Если обычный определенный интеграл представлен числом (или площадью в геометрической интерпретации), то интегралы с переменными пределами являются функциями этих пределов.

На рис. 4.8 показано два примера задания простых определенных интегралов с переменным верхним пределом (сверху) и обоими пределами интегрирования (снизу).

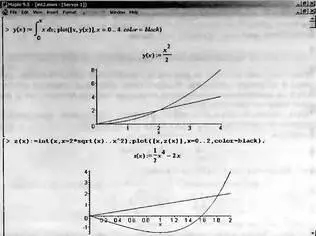
Рис. 4.8. Примеры интегралов с переменными пределами интегрирования

На этом рисунке построены также графики подынтегральной функции (это наклонная прямая) и функции, которую задаёт интеграл.

Функции int и Int могут использоваться для вычисления кратных интегралов, например, двойных и тройных. Для этого функции записываются многократно (файл intm):

> restart;

> Int(int(1/(x*y),x=4.0..4.4),y=2.0..2.6);

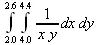
> value(%);

> Int(Int(Int((х^2+у^2)*z, x=0..a), y=0..a), z=0..a);

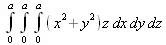
> value(%);

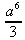
> Int(Int(2-х-у, x=sqrt(у)..у^2), у=0..1);

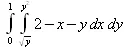
> value(%);

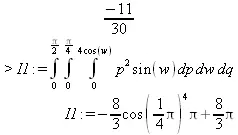
> evalf(I1);

Обратите внимание на нечеткую работу функции evalf в последнем примере. Эта функция уверенно выдает значение evalf(Pi) в форме вещественного числа с плавающей точкой, но отказывается вычислить значение интеграла, в которое входит число Pi. Этот пример говорит о том, что отдельные недостатки у Maple все же есть, как и поводы для ее дальнейшего совершенствования. В пакете расширения student имеются дополнительные функции интегрирования, которые дополняют уже описанные возможности. В частности, в этом пакете есть функции для вычисления двойных и тройных интегралов.

Maple открывает большие возможности в вычислении криволинейных, поверхностных и объемных интегралов. Нередко такие интегралы довольно просто заменяются на интегралы с переменными пределами интегрирования, что и иллюстрируют приведенные ниже примеры.

Пусть требуется вычислить объем фигуры, ограниченной координатными плоскостями и плоскостью х+ у + z= 1. Он, с учетом равенства z= 1-х-у, задается интегралом:

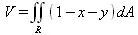
который заменяется следующим интегралом:

> Int(Int(1-х-у,у=0..1-х),х=0..1)=int(int(1-х-у,у=0..1-х),х=0..1);

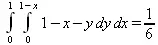
Последний, как видно, легко вычисляется.

Теперь вычислим массу указанной фигуры, которая задается тройным интегралом:

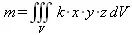
Здесь k — константа, характеризующая удельную площадь вещества. Этот интеграл также сводится к легко решаемому в Maple 9.5:

> m=Int(Int(Int(k*x*y*z,z=0..1-x-y),y=0..1-х),x=0..1);

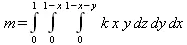
> value(%);

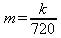
Специальные средства для вычисления подобных интегралов имеет пакет расширения VectorCalculus, который описывается в конце этой главы.

В составе самоучителей Maple 9.5 есть раздел Antiderivative, который иллюстрирует технику построения первообразной функции при интегрировании. Для доступа к окну этого инструмента (рис. 4.9) достаточно исполнить команду Tools→Tutors→Calculus-Single Variables→Antiderivative….

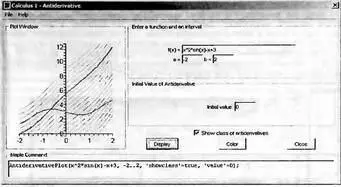
Рис. 4.9. Окно Maplet-демонстрации графиков функций и первообразных

Окно Maplet-демонстрэции интегрирования позволяет задать подынтегральную функцию и построить ее график и график первообразной функции, представляющей неопределенный интеграл. В окне а и b это не пределы интегрирования, а пределы изменения х при построении графиков. Опция Show class of antiderivatives позволяет построить графики множества первообразных, с выделением графика первообразной функции для заданного начального значения Initial Value. По завершении работы с окном демонстрации графики выводятся в документ Maple 9.5 — рис. 4.10.

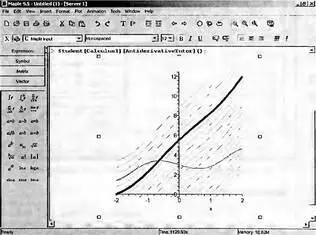
Рис. 4.10. Графики исходной функции и первообразных в окне документа Maple 9 5

Для демонстрации методов пошагового интегрирования имеется Maplet-инст-румент Step-by-step Integration Tutor. Для вызова его окна (рис. 4.11) нужно исполнить команду (в стандартном варианте интерфейса): Tools→Tutors→Calculus-Single Variables→Antiderivative….

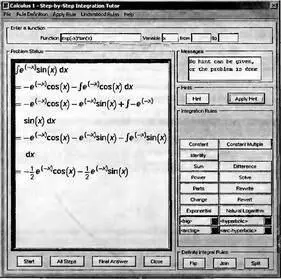
Рис. 4.11. Окно Maplet-демонстрации методов пошагового интегрирования