Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> taylor(1-ехр(х), х=1, 4);

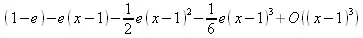
> convert(%,polynom);

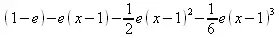
> taylor(sinh(x), x, 10);

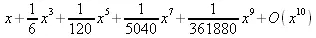
> taylor(int(sin(x)/x,x),x);

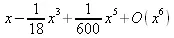
> taylor(erf(х),х);

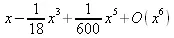
Не все выражения (функции) имеют разложение в ряд Тейлора. Ниже дан пример такого рода:

> taylor(1/х+х^2,х,5);

Error, does not have a taylor expansion, try series()

> series(1/х+х^2,x,10);

> taylor(1/х+х^2,x=1,5);

Здесь Maple 9.5 отказался от вычисления ряда Тейлора в окрестности точки х=0 (по умолчанию) и предложил воспользоваться функцией series. Однако эта функция просто повторяет исходное разложение. В то же время в окрестности точки х=1 ряд Тейлора вычисляется.

Для разложения в ряд Тейлора функций нескольких переменных используется библиотечная функция mtaylor:

mtaylor(f, v)

mtaylor(f, v, n)

mtaylor(f, v, n, w)

Здесь f — алгебраическое выражение, v — список имен или равенств, n — необязательное число, задающее порядок разложения, w — необязательный список целых чисел, задающих «вес» каждой из переменных списка v. Эта функция должна вызываться из библиотеки Maple 9 с помощью команды readlib:

> readlib(mtaylor); mtaylor(sin(х*у),[х,у],10,[2,1]);

> mtaylor(exp(-x)*sin(y),[x,y],5);

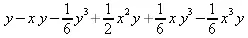
Для получения только коэффициента при k- м члене ряда Тейлора можно использовать функцию coeftayl(expr,var,k). Если expr — функция нескольких переменных, то k должен задаваться списком порядков коэффициентов.

Полезно сочетать разложение выражений (функций) в ряд Тейлора с графической визуализацией такого разложения. Рассмотрим документ, в котором наглядно показаны возможности представления функции рядами Тейлора и Маклорена.

На рис. 4.16 показана первая часть документа. Она дает пример разложения в ряд Тейлора функции sin(x) с построением ее графика и графика по разложению в ряд.

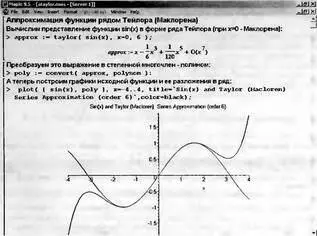
Рис. 4.16. Разложение функции sin(x) в ряд Маклорена шестого порядка и построение ее графика

Поскольку выбрано разложение относительно точки х=0, то полученный ряд является рядом Маклорена. Это хороший пример визуализации результатов математических вычислений — здесь наглядно видно, что при малых значениях x график ряда практически повторяет разлагаемую функцию, но затем начинает сильно от нее отходить.

Обратите внимание на следующее — несмотря на то, что мы задали шестой порядок ряда, последний член имеет только пятый порядок. Это связано со спецификой данного разложения — в нем просто отсутствуют члены четного порядка.

Можно буквально в считанные секунды попробовать изменить число членов ряда или диапазон изменения переменной х, что и показано на рис. 4.17 (вторая часть документа). При этом легко убедиться в том, что при больших x поведение ряда не имеет ничего общего с поведением разлагаемой в ряд функции — в частности, нет и намека на периодичность разложения, которая присуща тригонометрической функции sin(x).

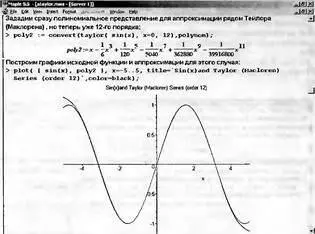
Рис. 4.17. Разложение функции sin(x) в ряд Маклорена 12-го порядка и построение ее графика

В заключительной (третьей) части этого документа (рис. 4.18) представлено уже истинное разложение синуса в ряд Тейлора в окрестности смешенной от нуля точки х=1. При смещении точки, относительно которой ведется разложение, выражение для ряда Тейлора существенно изменяется. В нем, во-первых, появляются члены четных степеней, а во-вторых, фигурирует аргумент вида (х-1) n.

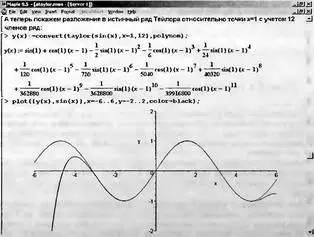
Рис. 4.18. Разложение функции sin(x) в ряд Тейлора 12-го порядка относительно точки x=1 и построение ее графика

Нетрудно заметить, что даже при представлении такой «простой» функции, как sin(x), приемлемая погрешность представления одного периода достигается при числе членов ряда Тейлора порядка 10 и более. Однако существенное повышение порядка ряда нецелесообразно из-за резкого возрастания вычислительных погрешностей. Впрочем, если задать достаточно большое число верных цифр результатов, то в Maple можно использовать ряды с гораздо большим числом членов.

Кроме того, серьезным недостатком аппроксимации рядом Тейлора является непредсказуемое поведение полинома вдали от точки, относительно которой задается представление. Это хорошо видно на всех трех приведенных примерах.

Помимо указанных выше разложений в ряд Maple имеет множество функций для иных разложений. Например, в пакете numapprox имеется функция laurent(expr,var,n), позволяющая получить разложение в ряд Лорана, функция chebyshev(expr, eq/nm, eps) дает разложение в форме полиномов Чебышева и т.д.

Степенные разложения часто используются в математических расчетах для приближенного представления разнообразных функций и обеспечения единообразия такого представления. В пакете powseries сосредоточены расширенные средства по реализации таких разложений. Пакет загружается командой:

> with(powseries):

Ниже представлено определение функций этого пакета:

compose(a.b) — объединяет ряды а и b;

evalpow(expr) — вычисляет выражение expr и возвращает его в виде ряда;

inverse(p) — инвертирует ряд р;

multconst(p,const) — умножает ряд p на константу const;

multiply(a,b) — умножает ряд а на ряд b;

negative(p) — возвращает аддитивный обратный по отношению к р ряд;

powadd(a,b,…) — складывает ряды а, b, …;

powcreate(expr) — создает ряд для выражения expr;

powpoly(pol,var) — создает ряд для полинома pol по переменной var;

powsolve(sys) — создает ряд для решения дифференциальных уравнений sys;

quotient(a.b) — возвращает частное для а и b в виде ряда;

reversion(a) — дает обратное к композиции разложение ряда а;

subtract(a.b) — дает разность рядов а и b.

В выражении expr могут использоваться операторы +, -, *, / и ^. С ними могут комбинироваться встроенные функции и функции пользователя, например fig). Кроме того, могут использоваться следующие функции: