Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

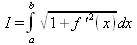
Для демонстрации вычисления длины дуги заданной аналитической функции имеется Maplet-инструмент ArcLench. Для вызова его окна (рис. 4.24) нужно исполнить команду (в стандартном варианте интерфейса): Tools→Tutors→Calculus-Single Variables→ArcLench….

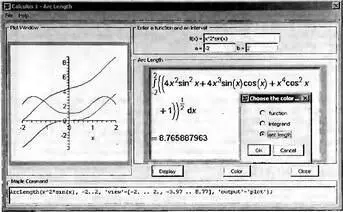
Рис. 4.24 Окно Maplet-инструмента для вычисления длины дуги

Данный инструмент по заданной функции f(x) и значениям а и b вычисляет длину дуги, выводит ее значение и вид интеграла, а также строит график функции, ее производной и зависимости длины дуги, начинающейся в точке а от текущего значения х, меняющегося от а до b. Соответствующие графики, отличающиеся цветом кривых, показываются в левой части окна инструмента.

Кнопка Color открывает окно выбора цвета из списка, который представлен окном Choose the color…, показанным внутри окна инструмента (см. рис. 4.24).

Выбрав цвет нужной кривой нажатие кнопки OK можно вызвать панель выбора цветов Select a color, показанную на рис. 4.25. По завершении выбора цвета нужная кривая будет отображена в новом цвете.

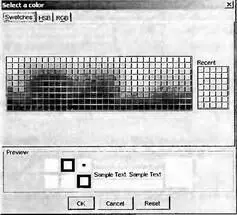
Рис. 4.25 Панель выбора цвета

Первая теорема о среднем гласит, что если f(x) интегрируемая функция, непрерывная на отрезке [a, b], то существует по крайней мере одно значение х=ξ в интервале [a, b], при котором

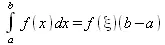
Иными площадь, определяемая интегралом может быть вычислена как площадь прямоугольника с основанием — отрезком ab и высотой f(ξ).

Для иллюстрации этого положения служит Maplet-инструмент Mean Value Theorem. Его окно (рис. 4.26) открывается исполнением команды Tools→Tutors Calculus-Single Variables→Mean Value Theorem… Работа с окном вполне очевидна. На графике строится кривая функции, отрезок, проходящий через ее концевые точки, точка со значением х=с=ξ и касательная к ней. Главный результат — значение с=ξ .

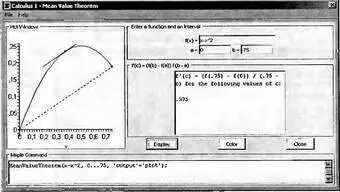
Рис. 4. 26. Окно Maplet-инструмента для иллюстрации первой теоремы о среднем

Для построения касательной к заданной точке на кривой f(x) служит Марlet-инструмент Tangent. Его окно (рис. 4.27) открывается исполнением команды Tools→Tutors→Calculus-Single Variables→Tangent…. Работа с окном вполне очевидна. На графике строится кривая функции и касательная к заданной точке х. Наклон касательной определяется значением первой производной f'(x), значение которой Slope и уравнений касательной вычисляются.

Рис. 4.27. Окно Maplet-инструмента для иллюстрации построения касательной к заданной точке

В некоторых случаях, например при реализации метода Ньютона решения нелинейных уравнений, помимо построения касательной к заданной точке кривой f(x) нужно строить секущие линии и определять их точки пересечения с f(x).

Для этого служит Maplet-инструмент Tangent and Secant. Его окно (рис. 4.28) открывается исполнением команды Tools→Tutors Calculus-Single Variables→Tangent and Secant…. Работа с окном вполне очевидна. На графике строится кривая функции и касательная к заданной точке х. Дополнительно строится ряд секущих. Возможно построение с применением анимации.

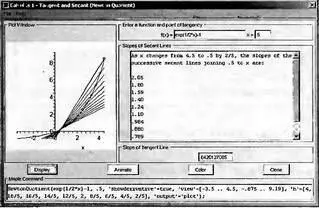
Рис. 4.28. Окно Maplet-инструмента для иллюстрации построения касательной к заданной точке и секущих линий

Пусть отрезок кривой f(х), при х в интервале [а,b] вращается вокруг оси 0х. Тогда площадь полученной фигуры вращения равна:

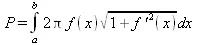
Для вычисления этой площади служит Maplet-инструмент Surface of Revolution. Его окно (рис. 4.29) открывается исполнением команды Tools Tutors→Calculus-Single Variables→Surface of Revolution…. Работа с окном вполне очевидна. На графике строится кривая функции и поверхность вращения этой кривой в 3D прямоугольной системе координат. Вычисляется значение площади. Вычисления возможны и при вращении отрезка кривой вокруг оси 0у.

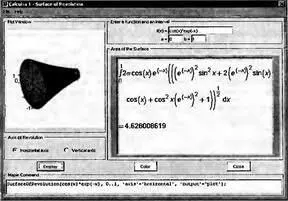
Рис. 4.29. Окно Maplet-инструмента для иллюстрации вычисления площади фигуры, полученной вращением отрезка кривой

Пусть отрезок кривой f(х), при х в интервале [a, b], вращается вокруг оси 0х. Тогда объем полученной фигуры вращения равен:

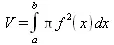
Для вычисления этого объема служит Maplet-инструмент Volume of Revolution. Его окно (рис. 4.30) открывается исполнением команды Tools→Tutors→Calculus-Single Variables→Volume of Revolution…. Работа с окном вполне очевидна. На графике строится кривая функции и поверхность вращения этой кривой в 3D прямоугольной системе координат. Вычисляется значение объема полученной фигуры. Вычисления возможны и при вращении отрезка кривой вокруг оси 0у.

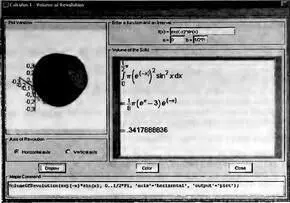
Рис. 4.30. Окно Maplet-инструмента для иллюстрации вычисления объема фигуры, полученной вращением отрезка кривой

Одиночное нелинейное уравнение , например трансцендентное, можно задать в одной из двух форм:

F(x) = 0 или f(x) = expr ,

expr — выражение. Второе уравнение всегда можно представить в виде F(x)=f(x)-expr= 0, то есть в форме первого уравнения.

При наличии аналитического решения оно находится путем поиска в ядре необходимых формул, описывающих такое решение. Но далеко не всегда нелинейные уравнения имеют аналитическое решение. В этом случае решение возможно численными методами.

Maple 9.5 имеет мощные средства для решение линейных и нелинейных уравнений и неравенств . Так, для решения линейных и нелинейных уравнений в аналитическом виде используется достаточно универсальная и гибкая функция