Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Нетрудно заметить, что это окно практически аналогично окну для демонстрации методов пошагового дифференцирования, описанному в разделе 4.3.4 (рис. 4.2). В связи с этим подробное описание средств этого инструмента можно опустить. Отметим лишь, что он позволяет задавать подынтегральную функцию и пределы интегрирования и по шагам (автоматически или вручную) вычислять интегралы. По окончании работы с окном соответствующий интеграл и результат его вычисления появляется в окне документа — рис. 4.12.

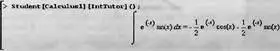
Рис. 4.12. Пример вывода результата работы с Maplet-инструментом по методам интегрирования

Для численного вычисления определенных интегралов используется функция evalf в сочетании с функциями Int или int:

evalf(Int(f, x=a..b, …))

evalf(Int(f, a..b, …))

evalf(Int(f, list-of-equations, …))

evalf(Int(f, list-of-ranges, …))

evalf(int(f, x=a..b))

Вместо многоточия могут использоваться различные опции, например, для задания метода вычислений. Могут использоваться комбинированные методы (аналитический с численным), ряд Maple-методов повышенной точности, методы предложенные группой NAG, метод Монте-Карло и др. Детали задания методов можно найти в справке. Ограничимся несколькими примерами вычисления определенных интегралов в численном виде (файл intnum):

> Int(х^2,х=1..2)=evalf(Int(х^2,х=1..2));

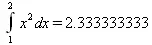
> Int(sin(x)/x,х=0..Pi)=evalf(int(sin(х)/х,х=0..Pi));

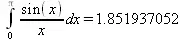
> Digits:=15;Int(sin(x)/x,x=0..Pi)=evalf(int(sin(x)/x, x=0..Pi, method = _NCrule));

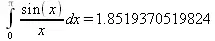
> expr := x*exp(-x):

Int(expr, x=1..infinity) = evalf[40](Int(expr, x=1..infinity, method=_Gquad));

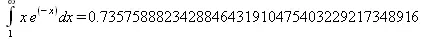
В двух последних примерах показано вычисление интегралов с повышенной точностью в 15 и 40 верных знаков. Аналогичным образом могут вычисляться и кратные интегралы.

На время и возможность вычисления определенных интегралов большое значение оказывает выбранный метод вычислений. Нередко его стоит указывать явно. Ниже приведены примеры этого с оценкой времени интегрирования (файл intmet):

> restart: t:=time(): int((1-ехр(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^2)/z^3,z=0.0..infinity); time()-t;

> t:=time(): evalf(Int((1-ехр(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^2)/z^3,z=0..infinity, Gquad)); time()-t;

> t: =time(): evalf(Int((1-exp(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^)/z^3,z=0.. infinity,_CCquad)); time()-t;

> t:=time(): evalf(Int((1-ехр(-z^2))/(BesselJ(1,z)^2+ BesselY(1,z)^2)/z^3,z=0..infinity,_Sinc)); time()-t;

> t:=time(): evalf(Int((1-ехр(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^2)z^3,z=0..infinity,_Dexp)); time()-t;

В данном случае лучшим оказался метод _Dexp (адаптивный двойной экспоненциальный метода). Разумеется, для других интегралов более целесообразным может оказаться применение другого метода. Приведенные значения времен интегрирования могут заметно отличаться при реализации вычислений на разных ПК. Данные выше приведены для ПК с процессором Pentium 4 НТ с рабочей частотой 2,6 ГГц.

Пределом функции f(х) называют то ее значение b, к которому функция неограниченно приближается в точке х=а (предел в точке) или слева или справа от нее. Пределы обозначается как:

Предел в точке a	Предел слева от точки a	Предел справа от точки а

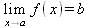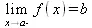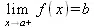При этом подразумевается, что функция f(x) определена на некотором промежутке, включающем точку х=а и во всех точках, близких к ней слева и справа. В последнем случае предел вычисляется для х=а-h или x=a+h при h стремящемся к нулю. Пределом может быть число, математическое выражение и положительная или отрицательная бесконечность. Последнее соответствует расширенному представлению о пределах.

Для вычисления пределов функции f в точке х=а используются следующие функции:

limit(f,x=a);

limit(f,x=a,dir);

Limit(f,x=a);

Limit(f,x=a,dir);

Здесь f — алгебраическое выражение, z — имя переменной, dir — параметр, указывающий на направление поиска предела (left — слева, right — справа, real — в области вещественных значений, complex — в области комплексных значений). Значением а может быть бесконечность (как положительная, так и отрицательная).

Примеры применения этих функций для вычисления пределов в точке приведены ниже (файл limit):

> restart: Limit(f(х),х=а);

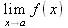
> Limit(1-ехр(-х), x=infinity)=limit(1-exp(-x), x=infinity);

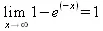
> Limit(exp(x),x=infinity) = limit(exp(x),x=infinity);

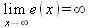
> Limit(exp(-x),x=infinity)=limit(exp(-x),x=infinity);

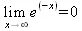
> Limit((x-sin(x))/x^3, x=0)=limit((x-sin(x))/х^3,х=0);

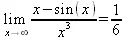
> Limit((Pi-2*x)*tan(x),x=Pi/2)=limit(tan(x)*(Pi-2*x), x=Pi/2);

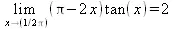
Обратите внимание на то, что в первом примере фактически дано обозначение предела в самом общем виде. Приведем еще пример вычисления предела функции в виде дроби, имеющей неопределенность 0/0:

> Limit((x-sin(х)) / (exp(2*х)-1-2*х-2*х^2),x=0) = limit((х-sin(x))/(exp(2*х)-1-2*х-2*х^2),х=0);

Как видно из этого примера, Maple «понимает» особенности функций при вычислении пределов.

Проверим возможности Maple при вычислении пяти замечательных пределов (файл limit5 — второй предел дан в двух вариантах):

> Limit(sin(х)/х,х=0)=limit(sin(х)/х,х=0);