Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
5.11.4. Прямое и обратное преобразование Фурье
Прямое преобразование Фурье преобразует функцию времени f(t) в функцию частот F(w) и заключается в вычислении следующей интегральной функции:
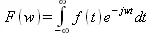
Оно в аналитическом виде реализуется следующей функцией пакета интегральных преобразований inttrans:
fourier(expr, t, w)
Здесь expr — выражение (уравнение или множество), t — переменная, от которой зависит expr, и w — переменная, относительно которой записывается результирующая функция.
Обратное преобразование Фурье задается вычислением интеграла
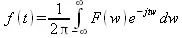
Оно фактически переводит представление сигнала из частотной области во временную. Благодаря этому преобразования Фурье удобны для анализа прохождения воздействий (сигналов) si(t) через устройства (цепи), заданные их частотной характеристикой K(w):
Здесь si(t) и so(t) — временные зависимости соответственно входного и выходного сигналов.
Определение (визуализация) преобразований Фурье и примеры их осуществления представлены ниже:
> restart:with(inttrans): assume(lambda>0,а>0):
> convert(fourier(f(t), t, s), int);
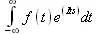
> convert(invfourier(f(t),t,s),int);
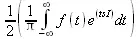
> fourier(sin(t),t,w);
> invfourier(%,w,t);
> fourier(1-exp(-a*t),t,w);
> invfourier(%,w,t);
> fourier(ln(1/sqrt(1+x^2)),x,y);
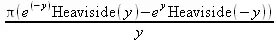
> fourier(BesselJ(n,x),x,y);
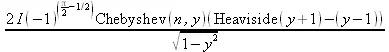
5.11.5. Вычисление косинусного и синусного интегралов Фурье
Разложение функции f(t) в ряд Фурье требует вычисления интегралов следующего вида:
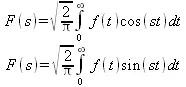
Они получили название косинусного и синусного интегралов Фурье и фактически задают вычисление коэффициентов ряда Фурье, в который может быть разложена функция f(t).
Для вычисления этих интегралов в пакете используются следующие функции:
fouriercos(expr,t,s)
fouriersin(expr,t,s)
Поскольку формат задания этих функций вполне очевиден, ограничимся примерами визуализации сути этих функций и примерами их применения:
> convert(fouriercos(f(t),t,s),int);
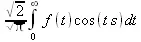
> convert(fouriersin(f(t),t,s),int);
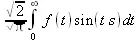
> fouriercos(5*t,t,s);
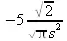
> fouriersin(5*t,t,s);
> fouriercos(exp(-t),t,s);
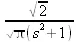
> fouriercos(arccos(х) * Heaviside(1-х), х, y);
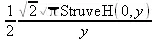
> fouriersin(arcsin(x) * Heaviside(1-х), x, y);
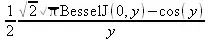
Нетрудно заметить, что эти преобразования нередко порождают специальные математические функции. Много примеров на преобразования Фурье содержатся в файле демонстрационных примеров fourier.mws.
5.11.6. Прямое и обратное преобразование Лапласа
Преобразования Лапласа — одни из самых часто применяемых интегральных преобразований. Они широко применяются в электрорадиотехнике и часто используются для решения линейных дифференциальных уравнений.
Прямое преобразование Лапласа заключается в переводе некоторой функции времени f(t) в операторную форму F(p). Это преобразование означает вычисление интеграла
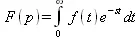
Для осуществления прямого преобразования Лапласа служит функция
laplace(expr,t,р)
Здесь expr — преобразуемое выражение, t — переменная, относительно которой записано expr, и p — переменная, относительно которой записывается результат преобразования.
Обратное преобразование Лапласа означает переход от функции F(p) к функции f(t) с помощью формулы
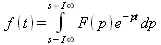
Для вычисления этого интеграла служит функция
invlaplace(expr, р, t)
где expr — выражение относительно переменной p, t — переменная, относительно которой записывается результирующая зависимость. Оба преобразования широко применяются в практике научно-технических вычислений и отражают суть операторного метода. При этом прямое преобразование создает изображение, а обратное — оригинал функции. Ниже приведены примеры определения и применения прямого и обратного преобразований Лапласа:
> restart:with(inttrans):
> convert(laplace(f(t),t,s), int);
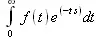
> laplace(sin(t)+a*cos(t),t,p);
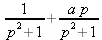
> invlaplace(%,р,t);
Нетрудно заметить, что в данном случае последовательное применение прямого, а затем обратного преобразования восстанавливает исходную функцию sin(t)+a cos(t). Преобразования Лапласа широко используются со специальными функциями и, в свою очередь, порождают специальные функции:
> laplace(FresnelC(t),t,p);
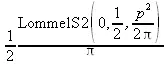
> laplace(Si(t)+Ci(t)+erf(t),t,p);
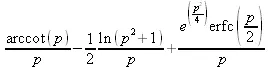
> laplace(BesselJ(0,t),t,p);
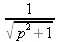
> invlaplace(1/sqr(р^2+1),t,р);
Интервал:
Закладка:










