Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Заметим, что этот результат относится только к конкретному ПК и может сильно меняться при прогонке этого примера на других. Так, читатель, знакомый с учебным курсом автора по системе Maple 7 [36] обнаружит, что там в этом примере результаты были иные и куда более ошеломляющие:

В чем дело? А дело в том, что более ранние результаты были получены в среде Maple 7 на компьютере с процессором Pentium II с частотой 400 МГц. А новые результаты получены уже на компьютере с процессором Pentium 4 с частотой 2,6 ГГц и с системой Maple 9.5.

Один из поводов разработки эффективной аппроксимации для вычисления математической функции заключается в создании библиотек подпрограмм для популярных языков программирования высокого уровня, таких как ФОРТРАН или С. В Maple имеются функции преобразования на любой из этих языков. Например, мы можем преобразовывать формулу для минимаксной аппроксимации в код ФОРТРАНа:

> fortran (MinimaxApprox(х));

Итак, нами показано, что правильный выбор аппроксимации для сложной функции обеспечивает уменьшение времени ее вычисления более чем на один-два порядка (!) при весьма приличной точности в 6 верных знаков и при использовании для вычислений минимального числа арифметических операций. Применение при этом средств системы Maple позволяет генерировать разложения в различные ряды, быстро вычислять рациональные аппроксимации функций и выполнять преобразования в различные специальные формы, сочетая это с мощными средствами интерактивной работы и графической визуализации, в частности с построением графиков функции и кривых ошибок при разных видах аппроксимации. Все это обеспечивает идеальную среду для решения таких задач.

Интегральные преобразования (см. файл inttrans) широко применяются в науке и технике. Так, прямое и обратное Z-преобразования функций широко используются при решении задач автоматического управления и обработке дискретных сигналов. Прямое Z-преобразование последовательности f(n) в функцию комплексной переменной z задается выражением:

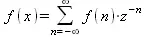
Обратное Z-преобразование сводится к преобразованию комплексной функции f(z) в функцию f(z).

Эти преобразования задаются следующими функциями:

ztrans(f, n, z) — прямое преобразование функции f(n) в f(z) ;

invztrans(f, z, n) — обратное преобразование f(z) в f(n) .

Заметим, что прямое Z-преобразование базируется на соотношении ztrans(f(n),n,z)=sum(f(n)/z^n,n=0..infinity), записанном на Maple-языке. В первых версиях системы Maple Z-преобразования выполнялись средствами библиотеки и требовали вызова командой readlib(ztrans). Но в Maple 7/8 они уже были включены в ядро системы и предварительного вызова уже не требуют. В этом убеждают следующие примеры:

> a:=ztrans(n^2,n,z);

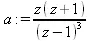
> invztrans(a,z,n);

> ztrans(cos(Pi/4*t), t, z);

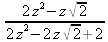
> invztrans(%,z,t);

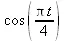
Нетрудно заметить, что в этих примерах функции, после прямого и обратного преобразований, восстанавливают свои значения.

Преобразование Фурье широко используется в математике, физике и электрорадиотехнике. Суть этого преобразования описана чуть ниже — см. раздел 5.11.4. Ввиду широких сфер применения этого преобразования в технике часто используется его особая разновидность — быстрое преобразование Фурье или FFT (Fast Fourier Transform).

В Maple на уровне ядра реализованы функции быстрого прямого FFT и обратного iFFT преобразований Фурье для числовых данных:

FFT(m, х, у)

evalhf(FFT(m, var(x), var(y)))

iFFT(m, x, y)

evalhf(iFFT(m, var(x), var(y)))

Здесь m — целое неотрицательное число, х и у — массивы с числом элементов, кратным степени 2 (например 4, 8, 16 и т.д.), представляющие действительные и мнимые части массива комплексных чисел (данных). Функции возвращают число элементов выходных массивов, а результат преобразований помещается в исходные массивы:

> х := array([1.,2.,3.,4.]): у := array([5.,6.,7.,8.]):

> FFT(2,х,y);

> print(х);

> print(y);

> iFFT(2,х,y);

> print(x);

> print(y);

Несмотря на высокую эффективность быстрых преобразований Фурье их недостатком является применение только к дискретно заданным численным данным, причем с числом отсчетов кратным двум в целой степени. Если данных меньше, недостающие элементы обычно заменяются нулями.

Альтернативой преобразований Фурье в наши дни стали вейвлет-преобразования. Вейвлеты это новый обширный базис для приближения произвольных зависимостей вейвлетами — «короткими» волночками разной формы, способными к масштабированию и перемещению. Вейвлеты прекрасно подходят для приближения локальных особенностей различных зависимостей, в том числе нестационарных (с параметрами, меняющимися во времени). Ознакомиться с вейвлетами и средствами работы с ними в системах MATLAB, Mathematica и Mathcad можно по книге [55]. К сожалению, в Maple готовые средства вейвлет-преобразований отсутствуют и это серьезный недостаток этих систем.

Для расширенной поддержки интегральных преобразований служит пакет inttrans

Это один из пакетов, наиболее важных для общематематических и научно-технических приложений. Он вызывается командой

> with(inttrans);

и содержит небольшой набор функций. Однако эти функции охватывают такие практические важные области математики, как ряды Фурье, прямые и обратные преобразования Лапласа и Фурье и ряд других интегральных преобразований. Ниже они обсуждены более подробно.