Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
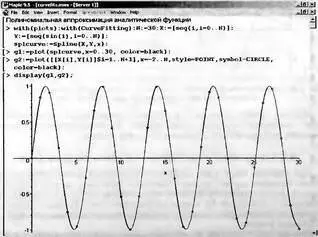
Рис. 5.22. Пример сплайновой аппроксимации синусоидальной функции
Здесь полезно обратить внимание на то, что за пределами области узловых точек значения, возвращаемые сплайновой функцией в пакете CurveFitting равны нулю. Так что экстраполяция по ней невозможна (в тоже время функция spline такой возможностью обладает).
5.9.6. Функция реализации метода наименьших квадратов LeastSquares
До сих пор мы рассматривали методы числовой аппроксимации функций или данных, при которых порядок полиномов определялся числом отсчетов функции.
Функция LeastSquares служит для реализации аппроксимации по методу наименьших квадратов. При этом методе происходит статистическая обработка данных (самих по себе или представляющих функцию) исходя из минимума среднеквадратической погрешности для всех отсчетов. Эта функция реализуется в формах:
LeastSquares(xydata, v, opts)
LeastSquares(xdata, ydata, v, opts)
Все входящие в нее параметры были определены выше (см. параметры функции BSplineCurve). Параметр opts задается в форме выражений weight=wlist, curve=f или params=pset.
Следующие примеры иллюстрируют применение функции LeastSquares:
> with(CurveFitting):
LeastSquares([[0,.5], [1,2], [2,4], [3,8]], v);
> LeastSquares([0,1,2,3], [1,2,4,6], v, weight-[1,1,1,10]);
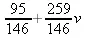
> LeastSquares([0,1,3,5,6], [1,-1,-3,0,5], v, curve=a*v^2+k*v+c);
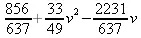
Наглядную иллюстрацию приближения группы точек кривой (в данном случае представленной полиномом четвертой степени) дает рис. 5.23. Кривая в облаке точек располагается таким образом, что площади квадратов над кривой и под ней в сумме равны нулю.
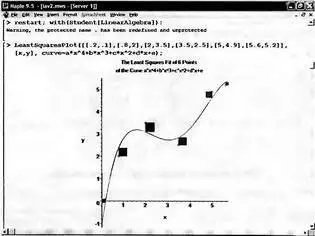
Рис. 5.23. Графическое представление метода наименьших квадратов
В конце этой главы мы вернемся к реализации метода наименьших квадратов при выполнении регрессионного анализа, построенного па этом методе.
5.9.7. Функция полиномиальной аппроксимации
Функция Polynomial Interpolation реализует полиномиальную интерполяцию и может использоваться в виде:
PolynomialInterpolation(xydata, v)
PolynomialInterpolation(xdata, ydata, v)
Параметры функции были определены выше. Параметр v может быть как именем, так и численным значением. Примеры применения функции представлены ниже
> with(CurveFitting):
PolynomialInterpolation([[0,0], [1,2], [2,4], [3, 3]], z);
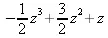
> PolynomialInterpolation([0, 2, 5, 8], [2, a, 1, 3], 3);
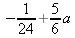
5.9.8. Функция рациональной аппроксимации
Функция рациональной интерполяции задается в виде:
RationalInterpolation(xydata, z, opts)
RationalInterpolation(xdata, ydata, z, opts)
где необязательный параметр opts задается выражениями method=methodtype или degrees=[d1,d2]. Функция возвращает результат в виде отношения двух полиномов.
Параметр methodtype может иметь значения lookaround или subresultant, задающие учет или пропуск сингулярных точек.
Пример применения функции RationalInterpolation (загрузка пакета опущена, но предполагается):
> xpoints := [0,1,2,3,4,-1]: ypoints := [0, 3, 1, 3, а, 1/11]:
f := RationalInterpolation(xpoints, ypoints, x);
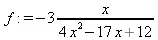
> for i from 1 to 6 do normal(eval(f,x=xpoints[i])-ypoints[i]) end do;
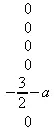
5.9.9. Функция вычисления обычных сплайнов Spline
Функция
Spline(xydata, v, opts)
Spline(xdata, ydata, v, opts)
вычисляет обычные (не В-типа) сплайны. Примеры ее применения даны ниже:
> Spline([[0,1], [1,2], [2,5], [3,3]], х);
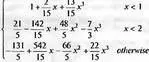
> Spline([0,1,2,3], [1,2,5,3], v, degree=1);
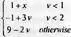
5.9.10. Функция аппроксимации непрерывными дробями
Функция ThieleInterpolation осуществляет интерполяцию на основе непрерывных дробей (Thiele's — интерполяцию). Она задается в виде:
ThieleInterpolation(xydata, v)
ThieleInterpolation(xdata, ydata, v)
Примеры применения данной функции представлены ниже:
> ThieleInterpolation([[1,3],[2,5],[4,75],[5,4]], х);
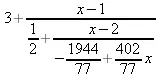
> ThieleInterpolation([1,2,а], [2,4,3], 3)
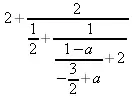
5.10. Выбор аппроксимации для сложной функции
5.10.1. Задание исходной функции и построение ее графика
Трудно представить себе область научно-технических расчетов более широкую и почитаемую, чем аппроксимация различных функциональных зависимостей. С получения простой аппроксимации сложной зависимости нередко начинаются (а часто и заканчиваются) научные исследования во многих областях как прикладной, так и фундаментальной науки. Покажем возможности в этом систем Maple на одном из комплексных примеров, давно помещенных в библиотеку пользователей системы Maple V R2, и переработанном для Maple 9.5/10. В этом примере используются многие из описанных выше средств приближения функций.
Воспользуемся ранее описанными возможностями пакета numapprox, для чего, прежде всего, подключим его:
> restart:with(numapprox):
Будем искать приемлемую аппроксимацию для следующей, отнюдь не простой, тестовой функции:
> f := х -> int(1/GAMMA(t), t=0..x ) / х^2;
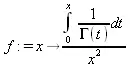
> plot(f,0..4,color=black);
График этой функции представлен на рис. 5.24. С первого взгляда это простой график, но тут как раз тот случай, когда простота обманчива. Вы сразу заметите, что график строится медленно, поскольку в каждой из множества его точек системе Maple приходится вычислять значение интеграла с подынтегральной функцией, содержащей довольно каверзную гамма-функцию. И делает это Maple по сложному и медленному алгоритму адаптивного численного интегрирования.
Читать дальшеИнтервал:
Закладка:










