Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Следующий пример иллюстрирует применение данной функции для аппроксимации функции erf(x):

> Digits:=12:w:=proc(х) 1.0 end;

> f:=proc(x) evalf(erf(x)) end;

> crit:=array(1..7, [0, .1,.25,.5,.75,.9,1.]);

> remez(w,f,0,1,5,0,crit,'maxerror');

> maxerror;

Отметим назначение других функций пакета numapprox:

chebdeg(p) — возвращает степень полинома Чебышева р;

chebmult(p, q) — умножение полиномов Чебышева p и q;

chebsort(e) — сортирует элементы ряда Чебышева;

confracform(r) — преобразует рациональное выражение r в цепную дробь;

confracform(r, х) — преобразует рациональное выражение r в цепную дробь с независимой переменной х;

hornerform(r) — преобразует рациональное выражение r в форму Горнера;

hornerform(r, х) — преобразует рациональное выражение r в форму Горнера с независимой переменной х;

infnorm(f, x=a…b, 'xmax') — возвращает L-бесконечную норму функции на отрезке х[а, b];

infnorm(f, a…b, "xmax") — возвращает L-бесконечную норму функции на отрезке [ а, b ].

Действие этих функций очевидно и читатель может самостоятельно опробовать их в работе.

Появившийся еще в Maple 7 пакет приближения кривых CurveFitting весьма полезен тем, кто занимается столь распространенной задачей, как приближение кривых. Он содержит ряд функций:

> with(CurveFitting);

Доступ к функциям пакета возможен с помощью конструкций:

CurveFitting[function](arguments) function(arguments)

Число функций пакета невелико и все они описаны ниже.

Функция BSpline(k, v, opt) служит для вычисления В-сплайнов. В отличии от обычных сплайнов, у которых точками стыковки сплайн-функций являются узловые точки, В-сплайны позволяют получить стыковку в произвольно заданных точках. Указанная функция имеет следующие параметры: k — порядок сплайна (целое число), v — имя и opt — параметр в виде knots=knotlist, где knotlist — список из k+ 1 элементов алгебраического типа. Используя функцию CurveFitting[BSplineCurve] можно строить кривые В-сплайнов. Примеры применения этой функции представлены ниже:

> BSpline(3, х);

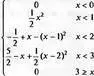
> BSpline(2, х, knots=[0,a,2]);

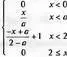
Как нетрудно заметить из этих примеров, функция Bspline возвращает результат в виде кусочных функций типа piecewise.

Функция BsplineCurve служит для построения кривых B-сплайнов. Она может использоваться в формах:

BSplineCurve(xydata, v, opts)

BSplineCurve(xdata, ydata, v, opts)

Здесь:

xydata — список, массив или матрица точек в форме [[х1,у1],[х2,у2],…,[хn,уn]];

xdata — список, массив или вектор значений независимой переменной [х1,х2,…,хn];

ydata — список, массив или вектор значений зависимой переменной в форме [у1,у2,…,уn];

v — имя независимой переменной;

opts — не обязательный параметр в форме одного или более выражений вида order=k или knots=knotlist.

Примеры применения функции BSplineCurve с порядком, заданным по умолчанию и с третьим порядком (кубический B-сплайн), представлены на рис. 5.19.

Следует отметить, что при малом числе точек стыковки аппроксимация B-сплайнами дает невысокую точность, что хорошо видно из рис. 5.19.

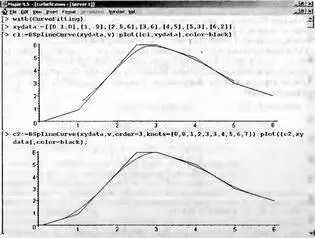
Рис. 5.19. Применение функции BSplineCurve

Когда аппроксимируется гладкая функция, представленная парами данных с равномерным расположением узлом, то данные как полиномиальной, так и сплайновой аппроксимаций различаются незначительно. В этом случае применение куда более сложной сплайновой аппроксимации, как правило, кажется мало обоснованным.

Однако если точки данных расположены неравномерно, то применение полиномиальной аппроксимации может оказаться совершенно неприемлемым. Это отчетливо показывает пример, представленный на рис. 5.20. Здесь задана на первый взгляд (судя по расположению точек) не слишком сложная и чуть колебательная зависимость. Однако полиномиальная аппроксимация (представлена тонкой кривой), особенно в начале — в интервале первых трех точек, дает явно ошибочные сильные выбросы. А вот сплайновая аппроксимация (показана более жирном линией) ведет себя куда более приемлемо.

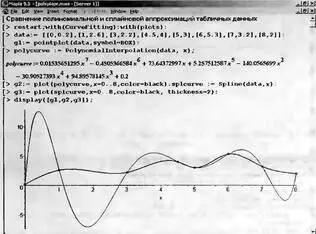
Рис. 5.20. Сравнение полиномиальной и сплайновой аппроксимаций для функции, заданной парами данных при неравномерном расположении узлов

Причина лучшего поведения сплайновой аппроксимации здесь вполне очевидна — напоминая поведение гибкой линейки, сплайновая функция эффективно сглаживает выбросы кривой в промежутках между точками.

При большом числе узлов (десятки-сотни и выше) данные представленные точками выглядят нередко не представительно. Например, на рис. 5.21 показан документ, иллюстрирующий сплайновую аппроксимацию функции синуса, представленной 31 отсчетом, но без вывода графика сплайновой функции. Несмотря на равномерное расположение узлов по графику точек невозможно определить, что это функция синуса.

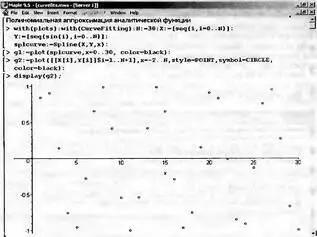
Рис. 5.21 Пример представления функции синуса 31 узловыми точками при равномерном расположении узлов

Рисунок 5.22 отличается от рис. 5.21 только построением сплайновой функции, представленной графическим объектом g1 (на рис. 5.19 он исключен из параметров функции display). После построения графика сплайновой аппроксимирующей функции становится вполне ясным, что точки представляют функцию синуса, которая прекрасно представляется отрезками полиномов сплайн-функции.