Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Функциональный ряд вида

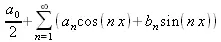(5.17)

называется тригонометрическим. Его коэффициенты а n и b n — действительные числа, не зависящие от х. Если этот ряд сходится для любого х из промежутка [-π, π], тогда он определяет периодическую функцию f(x) с периодом Т=2π. Ряд вида (5.17) называется рядом Фурье для интегрируемой на отрезке [-π, π] функции f(х), если коэффициенты его вычисляются по следующим правилам:

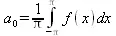(5.18)

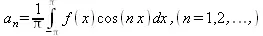(5.19)

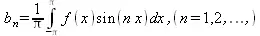(5.20)

В практических расчетах, как правило, ограничиваются конечным числом первых членов ряда Фурье. В результате получается приближенное аналитическое выражение для функции f(х) в виде тригонометрического полинома N- го порядка

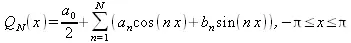
Но соотношения для вычисления коэффициентов Фурье (5.18)–(5.20) пригодны для случая аналитического задания исходной функции. Если функция задана в виде таблицы, то возникает задача приближенного отыскания коэффициентов Фурье по конечному числу имеющихся значений функции.

Таким образом, формулируется следующая задача практического, гармонического анализа: аппроксимировать на интервале (0, T) тригонометрический полином N- го порядка функцию у=f(х) , для которой известны m ее значений у k =f(х k ) при х k =kТ/m, где k= 0, 1, 2, …, m -1.

Тригонометрический полином для функции, определенной на интервале (0, Т), имеет вид:

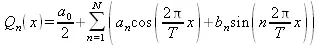(5.21)

Коэффициенты а nи b nопределяются следующими соотношениями:

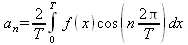(5.22)

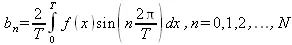(5.23)

Применяя в соотношениях (5.22)–(5.23) формулу прямоугольников для вычисления интегралов по значениям подынтегральных выражений в точках х k =kT/m , где k= 0, 1, 2, …, m- 1, имеем

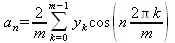(5.24)

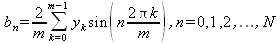(5.25)

Таким образом, тригонометрический полином (5.21), коэффициенты а nи b nнаходятся по формулам (5.24)–(5.25), служит решением поставленной задачи. При этом, коэффициенты (2.44)–(2.45) минимизируют сумму квадратов отклонений

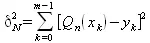
В случае, когда m=2N коэффициенты а nи b nдля n=0, 1, 2, …, N определяется соотношениями (5.24)–(5.25), а коэффициент a N определяется соотношением:

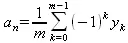
Сам же полином Q N (x) становится интерполяционным полиномом, так как в этом случае при любом b N выполняется соотношения Q N (x k )=y k для всех х k =kТ/m, где k = 0, 1, 2, …, m- 1.

В Maple 9.5 если функция задана аналитически, то наиболее простым способом нахождения ее аппроксимирующей зависимости является применение функции convert, которая позволяет представить функцию в виде иного выражения, чем исходное. Например, при опции polynom осуществляется полиномиальная аппроксимация. Это поясняют следующие примеры (файл aprox):

> convert(taylor(exp(х),х,5),polynom);

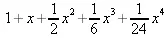
> f:=х->(х^3+х)/(х^2-1);

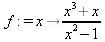
> convert(f(x),parfrac, x);

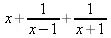
На рис. 5.9 представлен пример полиномиальной аппроксимации хорошо известной статистической функции erfc(x). Для полинома задана максимальная степень 12, но ввиду отсутствия в разложении четных степеней максимальная степень результата оказывается равна 11.

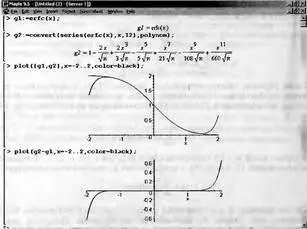
Рис. 5.9. Пример полиномиальной аппроксимации функции erfc(x) — сверху построены графики исходной функции и полинома, снизу график абсолютной погрешности

Как видно из приведенного рисунка, в интервале изменения x от -1,4 до 1,4 аппроксимирующее выражение почти повторяет исходную зависимость. Однако затем график аппроксимирующей функции быстро отходит от графика исходной зависимости и погрешность аппроксимации резко возрастает. При этом он ведет себя иначе даже качественно, никоим образом не показывая асимптотическое поведение, характерное для исходной зависимости. Это говорит о том, что полиномиальная аппроксимация плохо подходит для экстраполяции (предсказания) зависимостей.

Как уже отмечалось, считается, что полиномиальная аппроксимация дает большую погрешность при степени полинома более 5–6. Однако, этот вывод базируется на том, что большинство вычислительных программ работает всего с 5–10 точными знаками в промежуточных и окончательных результатах.

Maple по умолчанию имеет 10 точных знаков чисел. Это показывает следующий пример:

> restart:Digits;

Таким образом, Maple, как и любая другая программа может давать большую погрешность при высоких степенях аппроксимирующего полинома.

В этом убеждает рис. 5.10, на котором представлена программа полиномиальной аппроксимации функции синуса с возможностью выбора степени полинома N. Программа автоматически задает N+ 1 отсчетов функции синуса и затем выполняет ее полиномиальную аппроксимацию для N= 10 и Digits=8. Результат аппроксимации совершенно неудовлетворительный — видно, что программа под конец пошла вразнос — так именуются хаотические изменения кривой аппроксимирующей функции.