Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Итак, при задании f(х 1), …, f(х n) приближение к f(x) ищется в виде

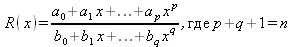(5.11)

Коэффициенты а i, b iнаходятся из совокупности соотношений R(х j)=f(x j) (j=1,…,n), которые можно записать в виде

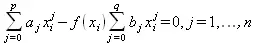
Данное уравнение образует систему n линейных уравнений относительно n+1 неизвестных. Такая система всегда имеет нетривиальное решение.

Функция R(x) может быть записана в явном виде в случае n нечетное, если р=q, и n четное, если р-q=1. Для записи функции R(x) в явном виде следует вычислять так называемые обратные разделенные разности, определяемые условиями

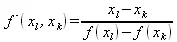
и рекуррентным соотношением

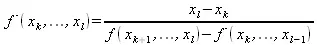
Интерполирование функций рациональными выражениями обычно рассматривают на основе аппарата цепных дробей. Тогда интерполирующая рациональная функция записывается в виде цепной дроби

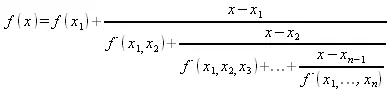
Использование рациональной интерполяции часто целесообразнее интерполяции полиномами в случае функций с резкими изменениями характера поведения или особенностями производных в точках.

При обработке экспериментальных данных, полученных с некоторой погрешностью, интерполяция становиться неразумной. В этом случае целесообразно строить приближающую функцию таким образом, чтобы сгладить влияние погрешности измерения и числа точек эксперимента. Такое сглаживание реализуется при построении приближающей функции по методу наименьших квадратов.

Рассмотрим совокупность значений таблично заданной функции f i в узлах х i при i=0,1,…,n. Предположим, что приближающаяся функция F(x) в точках х 1, х 2, …, х nимеет значения 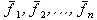. Будем рассматривать совокупность значений функции f(x) и функции F(x) как координаты двух точек n-мерного пространства. С учетом этого задача приближения функции может быть определена другим образом: найти такую функцию F(x) заданного вида, чтобы расстояние между точками M(f 1 , f 2 , …, f n ) и 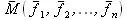было наименьшим. Воспользовавшись метрикой евклидова пространства, приходим к требованию, чтобы величина

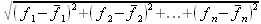
была наименьшей, что соответствует следующему:

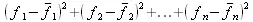(5.12)

то есть сумма квадратов должна быть наименьшей. Задачу приближения функции f(х) теперь можно формулировать иначе. Для функция f(х), заданной таблично, необходимо найти функцию F(x) определенного вида так, чтобы сумма квадратов (5.12) была наименьшей.

Выбор класса приближающихся функций определяется характером поведения точечного графика функции f. Это могут быть линейная зависимость, любые элементарные функции и т.д.

Практически вид приближающей функции F можно определить, построив точечный график функции f(х), а затем построить плавную кривую, по возможности наилучшим образом отражающую характер расположения точек. По полученной кривой выбирают вид приближающей функции.

Когда вид приближающей функции выбран, то последующая задача сводится к отысканию значений параметров функции. Рассмотрим метод нахождения параметров приближающей функции в общем виде на примере приближающей функции с тремя параметрами f=F(x, с, b, с). Тогда имеем

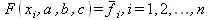(5.13)

Сумма квадратов разностей соответствующих значений функций f и F будет иметь вид:

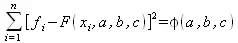(5.14)

Сумма (5.14) является функцией φ(a, b, с) трех переменных a, b, с. Задача сводится к отысканию ее минимума. Для этого используем необходимое условие экстремума:

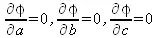
или

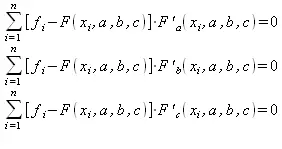(5.15)

Решив эту систему (5.15) трех уравнений с тремя неизвестными относительно параметров a, b , с, получим конкретный вид искомой функции F(x, a, b, с) . Изменение количества параметров не приведет к изменению сущности метода, а отразится только на количестве уравнений в системе (5.15).

Как следует из начальных условий, найденные значения функции F(x, а, b, с) в точках x 1, х 2, …, х nбудут отличаться от табличных значений y 1 , у 2 , …, у n . Значение разностей

будет определять отклонение измеренных значений f от вычисленных по формуле (5.14). Для найденной эмпирической формулы (5.14) в соответствии с исходными табличными данными можно найти сумму квадратов отклонений

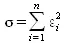(5.16)

Она, в соответствии с принципом наименьших квадратов для заданного вида приближающей функции и ее найденных параметров (параметры a, b, с ), должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя принципу наименьших квадратов, лучшим нужно считать тот, для которого сумма (5.16) имеет меньшее значение.

При тригонометрической интерполяции используются тригонометрические полиномы — линейные комбинации тригонометрических функций sin(nx) и cos(nx). Этот вид интерполирования применяется для процессов, которые отражают циклические процессы, связанные с периодическими функциями [52–54]. Известно, что такие функции удобно представлять в виде тригонометрического ряда или его частичной суммы с достаточной степенью точности.