Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
> S := Create(n+1,Kravchouk(n,p,q,x));
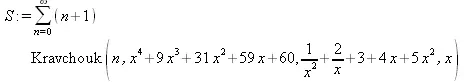
> ScalarMultiply(alpha, S);
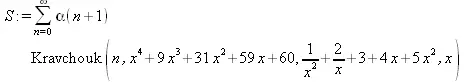
> simplify(%);
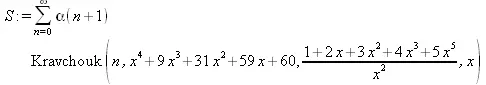
5.5. Пакет PolynomialTools
5.5.1. Обзор возможностей пакета PolynomialTools
Для выполнения ряда специальных операций с полиномами или создания полиномов с заданными свойствами служит пакет PolynomialTools. Этот пакет имеет небольшое число функций:
> with(PolynomialTools);
В пакет входят функции расщепления, сортировки и преобразования полиномов (в том числе в дифференциальные уравнения и наоборот) и др.
5.5.2. Функции для работы с полиномами
Рассмотрим несколько функций пакета PolynomialTools общего характера.
Функция IsSelfReciprocal(a, х, 'р') — проверяет полином а(х) на условие соeff(a,x,k)=coeff(a,x,d-k) для всех k=0..d, где d=degree(a, х) — порядок полинома. Если это условие выполняется, то возвращается логическое значение true, иначе — false. Если порядок d четный и если задан третий аргумент р, то р будет представлять полином P порядка d/2, такой, что x^(d/2)*P(x+1/x)=а. При нечетном d, полином а будет взаимо-обратным, что подразумевает деление на х+1. В этом случае если p указано, результат вычисляется в форме а/(х+1).
Примеры применения этой функции представлены ниже (файл poltools):
> with(PolynomialTools):
IsSelfReciprocal(х^4+х^3+х+1, x, 'p');
> p;
> IsSelfReciprocal(х^5-3*х^4+х^3+х^2-3*х+1, x, 'p');
> p;
> r := evalf(1+sqrt(2));
Функция MinimalPolynomial(r, n, acc) возвращает полином минимальной степени не превышающей n, имеющий корень r. Необязательный аргумент acc задает погрешность приближения. Функция MinimalPolynomial(r, n) использует решетчатый алгоритм и находит полином степени n (или менее) с наименьшими целыми коэффициентами. Корень r может быть действительным или комплексным. Результат зависит от значения переменной окружения Digits. По умолчанию acc задано как 10^(Digits-2). Примеры применения данной функции:
> MinimalPolynomial(r, 2);
> r := 1+sqrt(2);
> ( r, 2 );
> MinimalPolynomial( 1.234, 3 );
> fsolve( %, X );
Функция Split(a, х, b) служит для расщепления полинома а с независимой переменной х. Параметр b — не обязательный. Функция Split(a, х) осуществляет комплексную факторизацию инвариантного полинома а по х. Если третий аргумент b задан, он представляет множество элементов {t1, … ,tm}, таких что полином а расщепляется над K=Q(t1, …, tm), где Q означает поле рациональных чисел.
Примеры:
> Split(х^2+х+1,х);
> Split(х^2+у*х+1+у^2, x, 'b');
> b;
В пакете определена еще одна подобная функция Splits, с которой можно познакомиться по справке на нее.
Функция Translate(a, х, х0) преобразует полином а(х) с подстановкой х=х+х0, где х0 — константа. Примеры применения этой функции даны ниже:
> Translate(х^2, х, 1);
> expand(eval(х^2,х=х+1));
> Translate(х^3,х,2);
> expand(eval(х^3,х=х+2));
> Translate((х+1)^3,х,-1);
5.5.3. Функции сортировки полиномов
Для сортировки полиномов предназначены следующие три функции:
Shorter(f, g, х)
Sort(v, х)
Shorten(f, x)
Здесь f и g полиномы, v — список полиномов и x — независимая переменная. Функции отличаются характером сортировки.
Функция Shorter определяет полином f как более короткий, чем g, по следующим признакам: меньшая длина, меньшее имя независимой переменной х, не дробный и меньшая степень других переменных. Функция Sort сортирует лист полиномов х по признакам, определяемым Shorter. Функция Shorten использует преобразования Мёбиуса. Многочисленные детали ее применения можно найти в справке по данной функции. Примеры применения функций сортировки:
> Shorten(х^2+х+1,х);
> Shorten(3*х^3+18*х+14,х);
> Shorten(х^4+32);
> Shorter(х^3,х+5,х);
> Sort([х^3,х^2,х+1,х+5]);
Error, (in sort_poly) sort_poly uses a 2nd argument, x, which is missing
> Sort([х^3,х^2,x+1,x+5],x);
5.5.4. Функции преобразования полиномов в PDE и обратно
Функция PolynomialToPDE(polys, vars, depvars) преобразует полиномы polys по независимым переменным vars в дифференциальные уравнения с частными производными (PDE). Другая функция PDEToPolynomial(pdes, vars, depvars) осуществляет обратное преобразование. Следующие примеры иллюстрируют применение этих функций:
> S:= PolynomialToPDE([(х^2 - 2*х + 1)*u + x^3*v], [х], [u,v]);
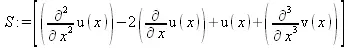
> PDEToPolynomial(S, [х], [u,v]);
5.6. Введение в интерполяцию и аппроксимацию
5.6.1. Основные понятия
Если некоторая зависимость y(х) представлена рядом табличных отсчетов y i(х i), то интерполяцией принято называть вычисление значений y(х) при заданном х, расположенном в интервале между отсчетами. За пределами общего интервала определения функции [ a, b ], то есть при x и x>b вычисление y(x) называют экстраполяцией (или, иногда, предсказанием значений функции). В данном случае речь идет об одномерной интерполяции, но возможны двумерная интерполяция функций двух переменных z(х, у) и даже многомерная интерполяция для функций многих переменных.
Интерполяция и экстраполяция часто выполняются по некоторой скрытой, но подразумеваемой, зависимости. Например, если узловые точки функции соединить отрезками прямых, то будем иметь многоинтервальную линейную интерполяцию данных. Если использовать отрезки параболы, то интерполяция будет параболической. Особое значение имеет многоинтервальная сплайн-интерполяция, области применения которой уже сейчас весьма обширны и непрерывно расширяются. Интерполяция рядом Фурье (набором синусоидальных функций) также достаточно хорошо известна, она эффективна при интерполяции периодических функций.
Читать дальшеИнтервал:
Закладка:










