Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
> coeff(р,х^3);
> coeff(р,х,4);
> coeffs(p,x);
> q:=x^2+2*y^2+3*x+4*y+5;
> coeffs(q);
> coeffs(q,y);
> coeffs(q,x,y);
> collect(q,x);
> collect(q,x,y);
Дополнительные примеры на применение функции collect можно найти в файле collect.
5.3.3. Оценка коэффициентов полинома по степеням
Полином может быть неполным, то есть не содержать членов со степенями ниже некоторой. Функция lcoeff возвращает старший, а функция tcoeff — младший коэффициент полинома нескольких переменных. Эти функции задаются в виде:
lcoeff(р)
tcoeff(р)
lcoeff(р, х)
tcoeff(р, х)
lcoeff(р, х, 't')
tcoeff(р, х, 't')
Функции lcoeff и tcoeff возвращают старший (младший) коэффициент полинома р относительно переменной х или ряда переменных при многомерном полиноме. Если х не определено, lcoeff (tcoeff) вычисляет старший (младший) коэффициент относительно всех переменных полинома p. Если третий аргумент t определен, то это имя назначено старшему (младшему) члену p. Если х — единственное неизвестное, и d — степень p по х, то lcoeff(p, x) эквивалентно coeff(p, x, d). Если х — список или множество неизвестных, lcoeff (tcoeff) вычисляет старший (младший) коэффициент p, причем p рассматривается как полином многих переменных. Имейте в виду, что p должен быть разложен по степеням неизвестного x до вызова функций lcoeff или tcoeff.
Приведем примеры применения функций lcoeff, tcoeff и coeffs (файл polan):
> q:=1/x^2+2/x+3+4*x+5*x^2;
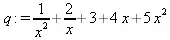
> lcoeff(q,x);
> lcoeff(q,x,'t');
> t;
> coeffs(q,x,'t');
> t;
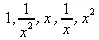
5.3.4. Оценка степеней полинома
Функция degree возвращает высшую степень полинома, a ldegree — низшую степень. Эти функции задаются следующим образом:
degree(а,х)
ldegree(а, х)
Функции degree и ldegree используются, чтобы определить высшую и низшую степень полинома от неизвестного (неизвестных) х, которое чаще всего является единственным, но может быть списком или множеством неизвестных. Полином может иметь отрицательные целые показатели степеней при х. Таким образом, degree и ldegree могут возвратить отрицательное или положительное целое число. Если выражение не является полиномом от x сданным параметром, то возвращается FAIL.
Чтобы degree и ldegree возвратили точный результат, полином обязательно должен быть сгруппирован по степеням х. Например, для выражения (x+1)(х+2)-x^2 функция degree не обнаружит аннулирование старшего члена и неправильно возвратит результат 2. Во избежание этой проблемы перед вызовом degree следует применять к полиному функции collect или expand. Если х — множество неизвестных, degree/ldegree вычисляет полную степень. Если х — список неизвестных, degree/ldegree вычисляет векторную степень. Векторная степень определяется следующим образом:
degree(р,[]) = 0
degree(р,[x1,х2,...]) = degree(р,x1)
degree(lcoeff(р,x1),[х2,...])
Полная степень тогда определяется следующим образом:
degree(р, {x1, ...,xn}) = maximum degree(р,{x1,...xn))
или
degree(р,{x1,...,xn}) = degree(p,[x1,...,xn])
Обращаем внимание на то, что векторная степень зависит от порядка перечисления неизвестных, а полная степень не зависит. Примеры применения функций degree и ldegree:
> restart;
> р:=а4*х^4+a3*х^3+а2*х^2;
> degree(р,х);
> ldegree(р,х);
> q:=1/х^2+2/х+3+4*х+5*х^2;
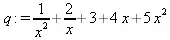
> degree(q,х);
> ldegree(q,х);
> degree(x*sin(x),x);
> zero := y*(x/(x+1)+1/(x+1)-1);
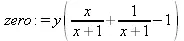
> degree(zero,x);degree(zero, y);
> degree(collect(zero,x,normal),x);degree(collect(zero,y, normal),y);
5.3.5. Контроль полинома на наличие несокращаемых множителей
Для контроля того, имеет ли полином несокращаемые множители, может использоваться функция irreduc(p) и ее вариант в инертной форме lreduc(p,K), где K — RootOf-выражение. Ниже приведены примеры применения этих тестовых функций:
> irreduc(х^2-1);
> irreduc(х^2-2);
> Irreduc(2*x^2+6*x+6) mod 7;
> Irreduc(x^4+x+1) mod 2;
> alias(alpha=RootOf(x^4+x+1)):
> Irreduc(х^4+х+1,alpha) mod 2;
5.3.6. Разложение полинома по степеням
Для разложения полинома р по степеням служат инертные функции AFactor(p) и AFactors(p). Полином может быть представлен в виде зависимости от одной или нескольких переменных.
Функция Afactor(p) выполняет полную факторизацию (разложение) полинома p от нескольких переменных с коэффициентами в виде алгебраических чисел над полем комплексных чисел. При этом справедливо отношение evala(AFactor(p))= factor(p.complex). Таким образом, эта функция является, по существу, избыточной.
В случае одномерного полинома полное разложение на множители является разложением на линейные множители. Функция AFactors аналогична функции Afactor, но создает структуру данных формы [u,[[f[1],e[1]],…,[f[n],e[n]]]] так, что p=u*f[1]^e[1]*…*f[n]^e[n], где каждый f[i] — неприводимый полином.
Ниже даны примеры применения функции Afactor:
> evala(AFactor(2*х^2+4*х-6));
> evala(AFactor(х^2+2*у^2));
> expand((x-1) * (x-2) * (x-3) * (x-4));
> AFactor(%);
> evala(%);
> expand((x-1+I*2)*(x+1-I*2)*(x-3));
Интервал:
Закладка:










