Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Для анализа функциональных зависимостей Maple 9.5 имеет специальный Maplet-Инструмент. Он вызывается командой Tools→Tutors→Calculus-Single Variable→Curve Analysis…. Она открывает окно инструмента, показанное на рис. 5.4.

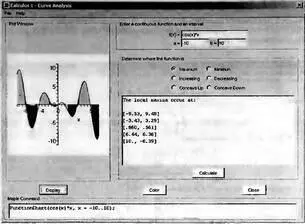
Рис. 5.4. Окно Maplet-инструмента анализа функциональных зависимостей

В верхней правой части окна имеются панели для ввода функциональной зависимости f(x) и границ а и b изменения аргумента х. Под ними имеется набор опций для задания того или иного параметра кривой, например ее максимумов Maximum, минимумов Minimum и др. После нажатия клавиши Calculate вычисляются координаты характерных точек или области определения тех или иных особенностей кривой.

График анализируемой кривой появляется в левой части окна. В нем строятся точки корней, перегибов и экстремумов зависимости. Цветом выделяются участки, на которых зависимость нарастает или падает. Кнопка Display порождает запись команды, которая строит полученный рисунок.

Для создания функций, составленных из отдельных кусков — кусочных функций, Maple 9.5 располагает интересной и по своему уникальной функцией:

piecewise(cond_1,f_1, cond_2,f_2, ..., cond_n,f_n, f_otherwise)

где f_i — выражение, cond_i — логическое выражение, f_otherwise — необязательное дополнительное выражение. В зависимости от того или иного условия эта функция позволяет формировать соответствующую аналитическую зависимость. К кусочным функциям (подчас в скрытой форме) приводят функции с элементами сравнения аргумента, например abs, signum, max и др. Поэтому в Maple 8 введен достаточно мощный аппарат обработки и преобразований таких функций по частям.

Рис. 5.5 показывает задание функции f(х), содержащей три характерных участка. По определенной через функцию пользователя зависимости f(х) можно, как обычно, построить ее график.

Рис. 5.5. Пример задания и применения функции, составленной из отдельных кусков

Важно отметить, что созданная с помощью функции piecewise зависимость может участвовать в различных преобразованиях. Например, на рис. 5.3 показано, что она легко дифференцируется и интегрируется, так что можно построить графики производной этой функции и ее интегрального значения. При этом каждая часть функции обрабатывается отдельно.

С функциями типа piecewise можно работать как с обычными функциями. При этом необходимые операции и преобразования осуществляются для каждой из частей функции и возвращаются в наглядной форме.

Ниже приведен пример задания функции f в аналитической форме (файл piecewi):

> restart;

> f := max(х^2 - 2, x-1);

Для выявления характера функции воспользуемся функцией convert и создадим объект g в виде кусочной функции:

> g := convert(f, piecewise);

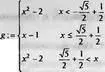
Выполним дифференцирование и интегрирование функции:

> fprime := diff(f, х);

> Int(g,х)=int(g,х);

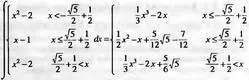
Как нетрудно заметить, результаты получены также в виде кусочных функций. Можно продолжить работу с функцией f и выполнить ее разложение в степенной ряд:

> series(f, х);

Чтобы убрать член с остаточной погрешностью, можно выполнить эту операцию следующим образом:

> series(g, х);

Обратите внимание на то, что поскольку разложение в ряд ищется (по умолчанию) в окрестности точки х= 0, то при этом используется только тот кусок функции, в котором расположена эта точка.

К числу наиболее известных и изученных аналитических функций относятся степенные многочлены — полиномы. Графики полиномов описывают огромное разнообразие кривых на плоскости. Кроме того, возможны рациональные полиномиальные выражения в виде отношения полиномов. Таким образом, круг объектов, которые могут быть представлены полиномами, достаточно обширен, и полиномиальные преобразования широко используются на практике, в частности, для приближенного представления других функций.

Под полиномом в СКМ сумма выражений с целыми степенями. Многочлен для ряда переменных — многомерный полином. К одномерным полиномам относятся степенной многочлен

а также отдельная переменная х и константа. Большое достоинство полиномов состоит в том, что они дают единообразное представление многих зависимостей и для своего вычисления требуют только арифметических операций (их число значительно сокращается при использовании хорошо известной схемы Горнера). Производные от полиномов и интегралы с подынтегральными функциями-полиномами легко вычисляются и имеют простой вид. Есть и достаточно простые алгоритмы для вычисления всех (в том числе комплексных) корней полиномов на заданном промежутке.

Для выделения коэффициентов полиномов в Maple служат следующие функции:

coeff(p, х) — возвращает коэффициент при х полинома p;

coeff(p, x, n) — возвращает коэффициент для члена со степенью n полинома p;

coeff(p, x^n) — возвращает коэффициенты при x^n полинома p;

coeffs(p, х, 't') — возвращает коэффициенты полинома нескольких переменных, относящиеся к переменной x (или списку переменных) с опцией 't', задающей имя переменной;

collect(p, x) — возвращает полином, объединяя коэффициенты при степенях переменной х.

Ниже даны примеры применения этих функций (файл coefcoll):

> р:=а4*х^4+а3*х^3+а2*х^2+а1*х+а0;

> coeff(р,х);