Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Примеры применения функции minimize приведены ниже (файл minmax):

> minimize(х^2-3*х+y^2+3*y+3);

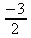
> minimize(х^2-3*х+y^2+3*y+3, location);

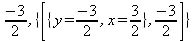
> minimize(х^2-3*х+y^2+3*y+3, х=2..4, y=-4..-2, location);

> minimize(х^2+y^2,х=-10..10,y=-10..10);

> minimize(х^2 + y^2,х=-10..10,y=-10..10, location);

> minimize(abs(х*ехр(-х^2)-1/2), х=-4..4);

> minimize(abs(х*ехр(-х^2)-1/2), х=-4..4, location=true);

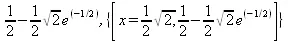
Приведем подобные примеры и для функции поиска максимума — maximize:

> maximize(х*ехр(-х));

> maximize(х*ехр(-х),location);

> maximize(sin(х)/х,х=-2..2,location);

> maximize(exp(-х)*sin(y),х=-10..10,y=-10..10, location);

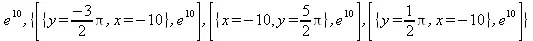
Обратите внимание на то, что в предпоследнем примере Maple 9.5 выдал верный результат, тогда как Maple 8 в этом примере явно «оскандалился» и вместо максимума функции sin(x)/x, равного 1 при x=0, выдал результат в виде бесконечности:

Эта ситуация кажется более чем странной, если учесть, что в этом примере еще Maple 6 давал правильный результат. Это еще один пример, показывающий, что в отдельных случаях Maple может давать неверные результаты.

Применим функцию minimize для поиска минимума тестовой функции Розенброка. Рис. 5.2 показывает, что minimize прекрасно справляется с данной задачей. На рис. 5.2 представлено также построение функции Розенброка, хорошо иллюстрирующее ее особенности.

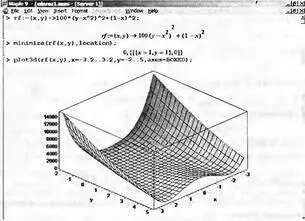
Рис. 5.2. Поиск минимума функции Розенброка и построение ее графика

Трудность поиска минимума функции Розенброка связана с ее характерными особенностями. Из рис. 5.2 видно, что эта функция представляет собой поверхность типа «глубокого оврага с почти плоским дном», в котором и расположена точка минимума. Такая особенность этой функции существенно затрудняет поиск минимума. То, что система Maple 9.5 справляется с данной тестовой функцией, вовсе не означает, что трудности в поиске минимума или максимума других функций остаются позади.

Часто необходимо найти минимум некоторой функции при наличии ограничений на значения независимых переменных. Ниже рассматривается нетривиальная задача такого рода, решаемая методом выпуклого программирования (разновидность нелинейного программирования) — файл minp.

Пусть надо найти минимум функции f:=х1^2+(х2–1)^2 при следующих ограничениях: 2x1+х2>=7, x1+2*х2>=5, x1>=0 и х2>=0. Составим на основе этого функцию Лагранжа:

> F:=x1^2+(х2-1)^2+y1*(7-2*х1-х2)+y2*(5-х1-2*х2);

и найдем ее частные производные:

> F1:=diff(F,x1);

> F2:=diff(F,x2);

> F3:=dxff(F,y1);

> F4:=diff(F,y2);

Соберем воедино все равенства и неравенства этой задачи:

> eq:={Fl=u1,F2=u2,x1*F1,x2*F2,F3+v1,F4+v2,y1*F3,y2*F4,

x1>=0,x2>=0,y1>=0,y2>=0,u1>=0,u2>=0,v1>=0,v2>=0};

Первые шесть равенств соответствуют теореме Куна-Такера о том, что в точке минимума существуют целые неотрицательные числа u1, u2 , v1 и v2 для которых выполняются эти шесть равенств (обратите внимание на то, что запись только левой части равенства означает, что она приравнивается к 0). Теперь с помощью функции solve можно найти решение данной задачи:

> solve(eq,{x1,х2,y1,y2,u1,u2,v1,v2});

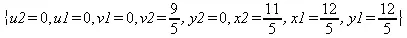
Таким образом, на указанном множестве функция достигает минимума в точке (12/5, 11/5).

Для исследования функций на непрерывность (отсутствие разрывов) Maple имеет функцию iscont, записываемую в ряде форм:

iscont(expr, х = а..b)

iscont(expr, х = а..b, 'closed')

iscont(expr, х = а..b, 'open')

Она позволяет исследовать выражение expr, заданное в виде зависимости от переменной х, на непрерывность. Если выражение непрерывно, возвращается логическое значение true, иначе — false. Возможен также результат типа FAIL. Параметр 'closed' показывает, что конечные точки должны также проверяться, а указанный по умолчанию параметр 'open' — что они не должны проверяться.

Работу функции iscont иллюстрируют следующие примеры (файл fanal):

> iscont(1/х^2,х=-1..1);

> iscont(1/х^2,х=-1..1,'closed');

> iscont(1/x,х=0..1);

> iscont(1/x,x=0..1,'closed');

> iscont(1/(x+a),x=-1..1);

Рекомендуется внимательно присмотреться к результатам этих примеров и опробовать свои собственные примеры.

Функции, не имеющие непрерывности, доставляют много хлопот при их анализе. Поэтому важным представляется анализ функций на непрерывность. Начиная с Maple 7, функция discont(f,x) позволяет определить точки, в которых нарушается непрерывность функции f(x). Она вычисляет все точки в пределах изменения х от –∞ до +∞. Результаты вычислений могут содержать особые экстрапеременные с именами вида _Zn~ и _NNn~. В частности, они позволяют оценить периодические нарушения непрерывности функций. Примеры применения функции discont приведены ниже (файл fanal):

> discont(1/(х-2),х);

> discont(1/((х-1)*(х-2)*(х-3)),х);

> discont(GAMMA(х/2),х);

Весьма рекомендуется наряду с применением данной функции просмотреть график анализируемой функции.