Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
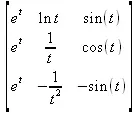
> Wronskian([t, t^2, t^3], t)
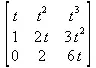
4.11.7. Функции теории поля
К основным функциям теории поля относятся:
Curl(F) — вычисляет вихрь векторного поля в R³;
Divergence(F) — вычисляет дивергенцию векторного поля;
Flux(f, dom) — вычисляет поток векторного поля в R³;
Gradient(f, с) — вычисляет градиент функции f в пространстве от R nдо R;
Del(f, с) и Nabla(f, с) — векторные дифференциальные операторы;
Laplacian(f, с) или Laplacian(F) — вычисляет лапласиан функции f или векторного определения (процедуры) F;
ScalarPotential(v) — вычисляет скалярный потенциал векторного поля;
Torsion(C, t) — вычисляет торсион в R³;
VectorPotential(v) — вычисляет векторный потенциал в R³;
Довольно громоздкие определения этих функций, основанные на использовании криволинейных и поверхностных интегралов, имеются в учебной литературе. Не приводя их, ограничимся приведенными ниже примерами применение указанных выше функций (файл vecft):
> restart:with(VectorCalculus): SetCoordinates('cartesian'[x,y,z]);
> F := VectorField( <-y,x,0> );
> Curl(F);
> Del &x F;
> Nabla &x F;
> CrossProduct(Del, F);
> F := VectorField(<���х^2,y^2,z^2>);
> Divergence(F);
> Flux(VectorField(, cartesian[x,y,z]), Sphere(<0,0,0>, r));
> Gradient(х^3/3+у^2, [x,y]);
> Del(х^2+у^2+z^2);
> Nabla(х^2+у^2+z^2);
> Del . %;
> Laplacian(х^2+у^2+z^2, [x,y,z]);
> Laplacian(f(r,theta,z));
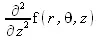
> SetCoordinates('cylindrical' [r, theta, z])
> Laplacian(f(r, theta, z));
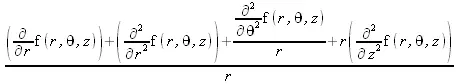
> SetCoordinates('cartesian'[x,y,z]);
> v := VectorField();
> ScalarPotential(v);
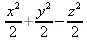
> v := VectorField(<-y,0,z>);
> ScalarPotential(v); den := х^2 + y^2 + z^2;
> ScalarPotential((x,y,z) -> /den);
> SetCoordinates('spherical'[r,phi,theta]);
> v := VectorField();
> ScalarPotential(v);
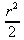
> restart:with(VectorCalculus): simplify( Torsion()) assuming t::real;
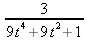
> Torsion(t -> <2*t,sin(t),cos(t)>);
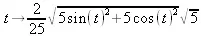
> SetCoordinates('cartesian'[x,y,z]); v := VectorField();
> VectorPotential(v);
> SetCoordinates('cylindrical'[r,theta,z]);
> v := VectorField();
> VectorPotential(v);
> simplify(Curl(%));
Обратите внимание на то, что для гарантии правильного выполнения этих команд и отсутствия «зависания» компьютера может потребоваться команда restart и перезагрузка пакета VectorCalculus.
4.11.8. Приближение площади сложной поверхности суммами Римана
Одним из важнейших приложений пакета VectorCalculus является вычисление длин дуг и площадей сложных поверхностей на основе применения линейных и поверхностных интегралов. Иногда это встречает большие трудности и требует специальных подходов. Примером может служить поверхность, заданная рис. 4.40. Эта поверхность построена с имитацией ее освещения от внешнего источника света.
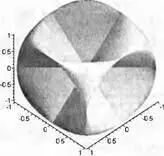
Рис. 4.40 Сложная поверхность с эффектами ее освещения внешним источником света
Применим обычную процедуру вычисления площади поверхности. Для этого вычислим для нее матрицу якобиана и удалим из нее столбец с нулевыми элементами (файл vecrim):
> J := Jacobian(f, [х, у, z]);
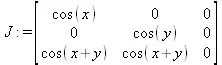
> J := DeleteColumn(J, [3]);
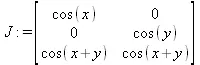
Тогда площадь поверхности вычисляется следующим образом:
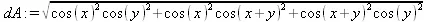
> Int(Int(dA, x=0..2*Pi), y=0..2*Pi);
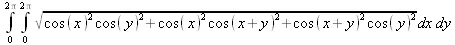
К сожалению, этот двойной интеграл Maple не вычисляет из-за сложности подынтегрального выражения, график которого представлен на рис. 4.41.
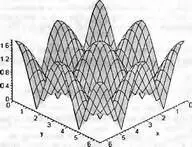
Рис. 4.41. График подынтегрального выражения
Для приближенного вычисления площади можно разбить поверхность на достаточное число сегментов и использовать замену интегралов суммами Римана. Оценка нижней и верхней сумм Римана для четверти поверхности (ее одного квадранта) представлена ниже:
> for s from 1 to 8 do
F := (k, t)->subs({x=k*Pi/(10*s), y=t*Pi/(10*s)}, dA):
A||s := evalf((Pi/<10*s))^2*sum(sum(F(p, q), p=0..10*s-1), q=0..10*s-1)):
print(A||s);
end do:
> for s from 1 to 8 do
F := (k, t)->subs({x=k*Pi/(10*s), y=t*Pi/(10*s)}, dA):
Alls := evalf((Pi/(10*s))^2*sum(sum(F(p, q), p=1..10*s),
q=1..10*s)):
print(A||s)
end do:
Поскольку эти суммы явно сходятся, то можно считать применение сумм Римана приемлемым и принять, что площадь данной поверхности приближенно равна:
> Area := 4*7.43;
4.11.9. Вычисление поверхностных интегралов
Приведенный выше пример иллюстрирует трудности вычислений поверхностных интегралов. Разумеется, далеко не всегда Maple требует специальных подходов к вычислению подобных интегралов и многие из них благополучно вычисляются.
Читать дальшеИнтервал:
Закладка:










