Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

middlesum — числовое приближение к интегралу центральными прямоугольниками;

midpoint — вычисление средней точки сегмента линии;

minimize — вычисление минимума функции;

powsubs — подстановка для множителей выражения;

rightbox — графическая иллюстрация интегрирования методом правых прямоугольников;

rightsum — числовое приближение к интегралу правыми прямоугольниками;

showtangent — график функции и касательной линии;

simpson — числовое приближение к интегралу по методу Симпсона;

slope — вычисление и построение касательной к заданной точке функции;

trapezoid — числовое приближение к интегралу методом трапеций;

value — вычисляет инертные функции.

В Maple 8/9 число функций этого пакета было несколько сокращено в сравнении с Maple 7, так что надо быть внимательным при его использовании в практических вычислениях — некоторые документы с функциями этого пакета, подготовленные в среде Maple 7, могут не работать в среде Maple 8/9/9.5.

В ядре и в пакетах расширения Maple 8/9/9.5 можно найти множество специальных функций для вычисления интегралов различного типа. Например, в пакете student имеются следующие функции:

Int(expr,x) — инертная форма вычисления неопределенного интеграла;

Doubleint(expr,x,у,Domain) — вычисление двойного интеграла по переменным х и у по области Domain;

Tripleint(expr,x,y,z) — вычисление тройного интеграла;

intparts(f,u) — интегрирование по частям.

Ниже дан пример применения функции Tripleint пакета student:

> Tripleint(f(х,у,z),х,у,z);

> Tripleint(х*у*z^2,x=0..2,y=0..3,z=0..5);

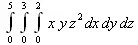
> evalf(%);

> int(int(int(x*y*z^2,x=0..2),y=0..3),z=0..5);

Пакет student имеет три графические функции для иллюстрации интегрирования методом прямоугольников:

leftbox(f(x), x=a..b, о) или leftbox(f(x), x=a..b, n, 'shading'=, о);

rightbox(f(x), x=a..b, о) или rightbox(f(x), x=a..b, n, o);

middlebox(f(x), x=a..b, о) или middlebox(f(x), x=a..b, n, o);

Здесь f(x) — функция переменной x, x — переменная интегрирования, a — левая граница области интегрирования, b — правая граница области интегрирования, n — число показанных прямоугольников, color — цвет прямоугольников, о — параметры (см. ?plot,options).

В этих функциях прямоугольники строятся соответственно слева, справа и посередине относительно узловых точек функции f(х), график которой также строится. Кроме того, имеется функция для построения касательной к заданной точке х = а для линии, представляющей f(x):

showtangent(f(х), х=а)

Рисунок 4.36 показывает все эти возможности пакета student. Четыре отмеченных вида графиков здесь построены в отдельных окнах.

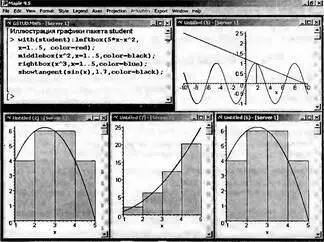
Рис. 4.36. Примеры иллюстративной графики пакета student

Графические средства пакета student ограничены. Но они предоставляют как раз те возможности, которые отсутствуют в основных средствах построения графиков. В Maple 9/9.5 функции пакета резко расширены и мы вернемся к их рассмотрению в Главе 9.

Пакет Student обеспечивает визуализацию ряда методов численного интегрирования: методов прямоугольников с различным расположением их, метода трапеций и метода парабол (Симпсона). Это возможно в символьном виде, например (файл intvis):

> with(student): middlesum(x*exp(-x), x=a..b);

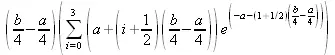
Ниже представлено несколько примеров такой визуализации (для метода прямоугольников со средним расположением их, метода трапеций и метода Симпсона):

> with(student): middlesum(х*exp(-x), x=0..4);

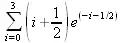
> trapezoid(х*ехр(-х), x=0..4);

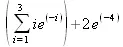
> simpson(x*sin(-х), х=1..4);

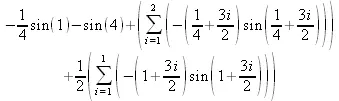
> evalf(%)

В последнем примере показано вычисление по представлению методом Симпсона.

Для работы с алгебраическими кривыми служит пакет расширения algcurves. Он загружается командами:

> restart;with(algcurves);

Ввиду важности функций пакета приведем полную форму записи и назначение наиболее важных функций этого пакета:

Weierstrassform(f,x,y,x0,y0,opt) — вычисление нормальной формы для эллиптических или гиперболических алгебраических кривых;

differentials(f, x, у, opt) — голоморфные дифференциалы алгебраических кривых;

genus(f,x,y,opt) — подлинность алгебраической кривой;

homogeneous(f,x,y,z) — создание полинома двух переменных, гомогенного в трех переменных;

homology(f, х, у) — находит канонический гомологический базис по алгоритму Треткоффа;

integral_basis(f, х, у, S) — интегральный базис алгебраического поля функции;

is_hyperelliptic(f, х, у) — тестирует кривую на ее принадлежность к гиперболической;

j_nvariant(f,x,y) — j-инвариант алгебраической кривой;

monodromy(f, х, у, opt) — вычисляет монодромию алгебраической кривой;

parametrization(f,x,y,t) — находит параметризацию для кривой с родом (даваемым функцией genuc), равным 0;

periodmatrix(f, х, у, opt) — вычисляет периодическую матрицу кривой;

plot_knot(f,x,y,opt) — строит узел — несамопересекающуюся замкнутую кривую в трехмерном евклидовом пространстве;

puiseux(f,x=p,y,n,T) — определяет Пуизе-расширение алгебраической функции (может иметь и более простые формы записи);

singularities(f,x,y) — анализирует кривую на сингулярность.

Приведем также примеры применения функций пакета Algcurves (файл algcurve):

> Weierstrassform((y^2-1)^2+x*(x^2+1)^2, x,y,x0,y0);

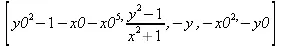
> f:=у^3+х^3*у^3+х^4;

> differentials(f, х, у);

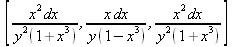
> differentials(f,x,у,skip_dx);

> nops(%);

> genus(f, x, y);

> homogeneous(f, x, y, z);

> g := y^3-х*y^2+2*2^(1/2)*y^2+х^2-2*2^(1/2)*х+2+y^6;

> integral_basis(g,x,y);

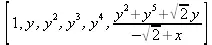
> is_hyperelliptic(f, x, y);

> f1:=у^2+х^5+1:is_hyperelliptic(f1, x, y);

> j_invariant(g,x,y);