Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
> SetCoordinates(cartesian);
> + m*;
> ( - ) / h;
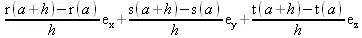
> limit(%,h=0);
Обратите внимание на вычисление предела в конце этих примеров. Далее можно отметить операцию точечного умножения, которая иллюстрируется следующими вполне очевидными примерами:
> . ;
> SetCoordinates(polar);
> . ;
> combine(%,trig);
> SetCoordinates(cartesian[x,y,z]);
> Del . VectorField(<���х^2,у^2,z^2>);
> Del . Del;
> (Del . Del) (f(x,y,z));
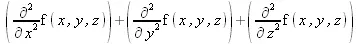
> L := VectorField( ) . Del;
> L(f(x,y,z));
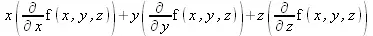
Определена также операция кросс-умножения:
> &х ;
> SetCoordinates(cylindrical);
> &x ;
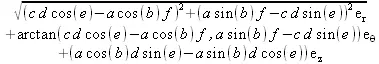
> SetCoordinates(cartesian[x,y,2]);
> Del &x VectorField( );
> L := VectorField() &x Del;
> L(f(x,y,2));
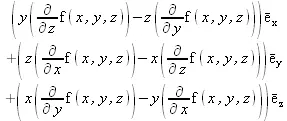
> L := Del &x Del;
> L(f(x,y,z));
4.11.4. Операции с кривыми
В пакете векторных операций определен ряд типовых операций с кривыми. Ниже представлено задание эллиптической кривой и вычисление в аналитической форме нормали и радиуса кривизны (файл vopcurves):
> SetCoordinates(cartesian);
> assume(t::real);
> ell := <2*cos(t),sin(t)>;
> nv := simplify(PrincipalNormal(ell,t));
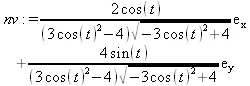
> len := simplify(LinearAlgebra:-Norm(nv, 2));
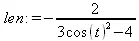
> r := simplify(RadiusOfCurvature(ell));
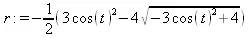
Теперь можно представить саму кривую (эллипс) и ее эволюту (рис. 4.39):
> ev := simplify(ell + r * nv / len);
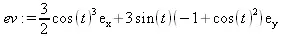
> plot([[ell[1], ell[2], t=0..2*Pi], [ev[1], ev[2], t=0..2*Pi]]);
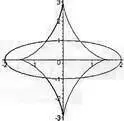
Рис. 4.39. Графики кривой — эллипса и ее эволюты
Нетрудно заметить, что для эллипса эволюта представляет собой удлиненную астроиду.
Для вычисления кривизны кривой С используется функция Curvature(C, t) в которой параметр t может и отсутствовать:
> Curvature(, t);
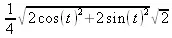
> с := Curvature(t -> ):
> simplify(c(t)) assuming t::real;
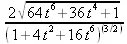
> SetCoordinates('polar');
> Curvature():
> simplify(%) assuming t::real;
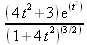
4.11.5. Интегрирование в пакете VectorCalculus
В аспекте практических приложений векторного анализа и теории поля особый интерес представляют приложения интегрирования пакете VectorCalculus. Так, видоизмененная функция int(f, dom) задает вычисление интеграла от функции f по области dom, например (файл vecint):
> restart:with(VectorCalculus):
> int(х^2+у^2, [x,y] = Circle(<0,1>, r));
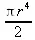
> int(sin(х)*cos(у)*tan(z), [x,y,z] = Parallelepiped(0..Pi, 0..Pi/3, 0..Pi/4));
Функция PathInt(f, dom) вычисляет интеграл пути для функции f с R nдо R:
> PathInt(х^2, [х,y] = Line(<0,0>, <1,2>));
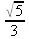
> PathInt(х^2+y^2, [х,y] = Circle(<0,0>, 3/2));
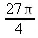
> PathInt(1, [х,y] = Ellipse(х^2+y^2/2-1));
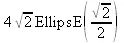
Другая функция LineInt(F, dom), где F — вектор или процедура задания векторного поля, dom — параметр, характеризующий направление интегрирования, задает вычисление линейного интеграла в пространстве R n:
> SetCoordinates(cartesian[х,y]);
> LineInt(VectorField(<���х,y>), Line(<0,1>, <2,-5>));
> LineInt(VectorField(), Circlet<0,0>, r));
> LineInt(VectorField(), Ellipse(х^2/4+y^2/9-1));
> LineInt(VectorField(), Arc(Ellipse(х^2/4+у^2/9-1), 0, Pi/2));
Функция ArcLength(C,dom) задает вычисление длины дуги С по известному интегральному выражению для нее:
> ArcLength(, t=0..Pi) assuming r>0;
> ArcLength(t -> , 0..2);
> evalf(%);
Рекомендуется просмотреть различные варианты задания области интегрирования dom в справке по этому пакету.
4.11.6. Задание матриц специального типа
Пакет VectorCalculus позволяет для заданной функции f задавать несколько матриц специального вида, которые часто используются при решении задач теории поля:
Hessian(f, t) — создание матрицы гессиана;
Jacobian(f, v, det) — создание матрицы якобиана;
Wronskian(f, t) — создание матрицы вронскиана.
Примеры задания таких матриц приведены ниже (файл vecmatrix):
> Hessian(ехр(х*y), [х,y]);
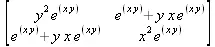
> Hessian(а/(х^2+y^2+z^2), [х, y, z]);
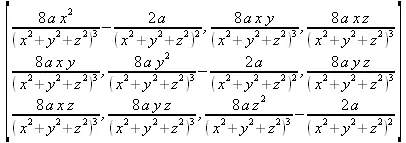
> Н := unapply(%, [a,x,y,z]):
> Н(1/2, 0.3, 0.7, 0.1);
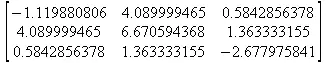
> Jacobian([r*cos(t), r*sin(t)], [r,t]);
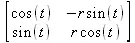
> Jacobian([r*cos(t), r*sin(t)], [r,t], 'determinant');
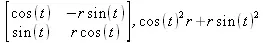
> Wronskian([exp(t),ln(t),sin(t)], t);
Интервал:
Закладка:










