Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> solve(eqns, {x});

> f := sin(x+y) — exp(x)*y = 0: g := x^2 - у = 2:

fsolve{{f,g},{x,y},{x=-1..1,y=-2..0});

Заметим, что локализация поиска корней в заданном интервале позволяет отыскивать такие решения, которые не удается получить с помощью функций solve и fsolve в обычном применении. В последнем из приведенных примеров дается решение системы нелинейных уравнений, представленных уравнениями f и g.

Чтобы еще раз показать различие между функциями solve и fsolve, рассмотрим пример решения с их помощью одного и того же уравнения erf(x) = 1/2:

> solve(erf(х)=1/2,х);

> fsolve(erf(x)=1/2);

Функция solve в этом случае находит нетривиальное решение в комплексной форме через функцию RootOf, тогда как функция fsolve наводит обычное приближенное решение.

Мы уже отмечали, что функция solve дает решение уравнения ехр(-х) = х в форме специальной функции Ламберта. Нетрудно заметить, что функция fsolve дает результат сразу в форме числа с плавающей точкой:

> restart;eq:=exp(-х)=х;sol:=fsolve(ехр(-х)=х,х);

Функция solve имеет ряд родственных функций. Одну из таких функций — fsolve — мы рассмотрели выше. В справочной системе Maple можно найти ряд и других функций, например rsolve для решения рекуррентных уравнений, isolve для решения целочисленных уравнений, msolve для решения по модулю m и т.д. Здесь мы рассмотрим решение уравнений важного класса — рекуррентных. Напомним, что это такие уравнения, у которых заданный шаг решения находится по одному или нескольким предшествующим шагам.

Для решения рекуррентных уравнений используется функция rsolve:

rsolve(eqns, fens)

rsolve{eqns, fens, 'genfunc'(z))

rsolve(eqns, fens, 'makeproc')

Здесь eqns — одиночное уравнение или система уравнений, fens — функция, имя функции или множество имен функций, z — имя, генерирующее функциональную переменную.

Ниже представлены примеры применения функции rsolve (файл rsolve):

> restart;

> rsolve(f(n)=-2*f(n-1)-f(n-2), f(k));

> rsolve({f(n)=-3*f(n-1)-2*f(n-2),f(1..2)=1), {f});

> rsolve({y(n)=n*y(n-1), y(0)=1),y);

> rsolve((y(n)*y(n-1)+y(n)-y(n-1)=0,у(0)=a},y);

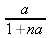
> rsolve({F(n)=F(n-1)+F(n-2),F(1..2)=1),F, 'genfunc'(x));

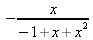
> rsolve({y(n+1)+f(n)=2*2^n+n, f(n+1)-y(n)=n-2^n+3, y(k=1..5)=2^k-1,f(5)=6), {y, f});

А теперь приведем результат вычисления функцией rsolve n-го числа Фибоначчи. Оно задается следующим выражением:

> eq1 := (f(n+2) = f(n+1) + f(n), f(0) = 1, f(1) = 1};

В нем задана рекуррентная формула для числа Фибоначчи — каждое новое число равно сумме двух предыдущих чисел, причем нулевое и первое числа равны 1. С помощью функции rsolve в Maple 9.5 можно получить поистине ошеломляющий результат:

> a1:=rsolve(eq1, f);

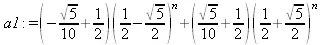
Числа Фибоначчи — целые числа. Поэтому представленный результат выглядит как весьма сомнительный. Но на самом деле он точный и с его помощью можно получить числа Фибоначчи (убедитесь в этом сами). Любопытно отметить, что решение в Maple8 заметно отличается от приведенного выше для Maple 9.5. Но только по форме, а не по сути.

Иногда бывает нужен результат в форме только целых чисел. Для этого используется функция isolve(eqns, vars), дающая решение в виде целых чисел. Приведем примеры ее применения (файл isolve):

> isolve({2*х-5=3*y});

> isolve(y^4-z^2*y^2-3*х*z*y^2-х^3*z);

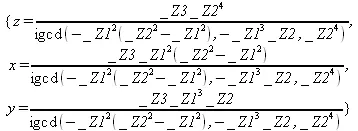
Здесь вывод представлен с помощью вспомогательных переменных _Z1.

Функция msolve(eqns,vars,m) или msolve(eqns,m) обеспечивает решение вида Z mod m (то есть при подстановке решения левая часть при делении на m дает остаток, равный правой части уравнения). При отсутствии решения возвращается объект NULL (пустой список).

Ниже даны примеры использования функции msolve (файл msolve):

> msolve{{3*х-4*y=1,7*х+y=2},12);

> msolve(2^i=3,19);

> msolve(8^j=2,х,17);

На этом мы завершаем рассмотрение функций системы Maple 9.5 для решения уравнений, неравенств и систем с ними.

Пакет student — это, несомненно, один из пакетов, наиболее привлекательных для студентов и аспирантов. В нем собраны наиболее распространенные и нужные функции, которые студенты университетов и иных вузов обычно используют на практических занятиях, при подготовке курсовых и дипломных проектов. Пакет вызывается командой:

> with(student);

Ниже представлено назначение функций этого пакета, включая некоторые функции из его более ранних версий:

D — дифференциальный оператор;

Diff — инертная форма функции вычисления производной;

Doubleint — инертная форма функции вычисления двойного интеграла;

Int — инертная форма функции интегрирования int;

Limit — инертная форма функции вычисления предела limit;

Lineint — инертная форма функции вычисления линейного интеграла lineint;

Point — тестирование объекта на соответствие типу точки (point);

Product — инертная форма функции вычисления произведения членов последовательности;

Sum — инертная форма функции вычисления суммы членов последовательности;

Tripleint — инертная форма функции вычисления тройного интеграла;

changevar — замена переменной;

combine — объединение подобных членов;

completesquare — вычисление полного квадрата (многочлена);

distance — вычисление расстояния между точками;

equate — создание системы уравнений из списков, таблицы, массивов;

extrema — вычисление экстремума выражения;

integrand — вывод подынтегрального выражения из под знака инертного интеграла;

intercept — нахождение точки пересечения двух кривых;

intparts — интегрирование по частям;

isolate — выделение подвыражения;

leftbox — графическая иллюстрация интегрирования методом левых прямоугольников;

leftsum — числовое приближение к интегралу левыми прямоугольниками;

makeproc — преобразование выражения в процедуру Maple;

maximize — вычисление максимума функции;

middlebox — графическая иллюстрация интегрирования метолом центральных прямоугольников;