Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
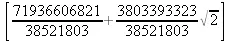
> parametrization(х^4+y^4+а*х^2*y^2+b*y^3,х,y,t);
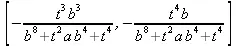
> Z := periodmatrix(f1,х,у,Riemann);
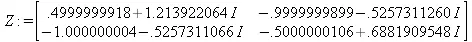
4.10.3. Построение алгебраических кривых класса knot
Функция plot_knot позволяет строить одну или несколько алгебраических кривых — узлов. Пример построения целого семейства узлов показан на рис. 4.37.

Рис. 4.37. Семейство узлов
Для лучшего обзора таких кривых рекомендуется воспользоваться возможностью вращения трехмерных фигур мышью для уточнения угла, под которым рассматривается фигура — в нашем случае семейство алгебраических кривых.
Начиная с версии Maple 7 в пакет расширения Algcurves добавлена новая функция импликативной графики plot_real_curve. Она строит алгебраическую кривую для действительной части полиномиального выражения и записывается в виде:
plot_real_curve(р, х, у, opt)
Функция имеет следующие параметры:
p — полиномиальное выражение переменных x и у задающее алгебраическую кривую;
opt — параметр, который может быть записан в форме приведенных ниже выражений:
showArrows=true или false — задает показ стрелок касательных или перпендикулярных к точкам вдоль кривой (по умолчанию false);
arrowIntervalStep=posint — задает число точек, пропускаемых до показа очередной пары стрелок (по умолчанию 10);
arrowScaleFactor=positive — задает масштаб для длины стрелок (по умолчанию 1);
colorOfTangentVector=с — задает цвет касательных стрелок, по умолчанию заданный как зелёный, COLOR(RGB,0,1.0);
colorOfNormalVector=с — задает цвет перпендикулярных стрелок, по умолчанию заданный как красный, COLOR(RGB,1,0,0);
colorOfCurve=с — задает цвет кривой, по умолчанию заданный как синий, COLOR(RGB, 0, 0, 1);
eventTolerance=positive — задает погрешность при представлении сингулярных точек (по умолчанию 0,01).
NewtonTolerance=positive — задает погрешность при выполнении ньютоновских итераций в ходе построений.
Функция plot_real_curve вычисляет и строит алгебраическую кривую по точкам. Применение функции plot_real_curve показывает рис. 4.38.

Рис. 4.38. Примеры применения функции plot_real_curve
4.11. Векторные вычисления и функции теории поля
4.11.1. Пакет векторных вычислений VectorCalculus
В Maple 8 были существенно расширены возможности вычислений над векторами (пространственными объектами) и поверхностями. Для этого введен пакет VectorCalculus, который, при вызове, открывает доступ ко многим командам и функция векторного анализа, теории поля и приложений дифференциального исчисления [67, 68] (файл vc):
> restart; with(VectorCalculus); interface(showassumed=0);
Warning, the assigned names <,> and <|> now have a global binding
Warning, these protected names have been redefined and unprotected:
*, +, Vector, diff, int, limit, series
Нетрудно заметить, что данный пакет после загрузки видоизменяет многие операторы, команды и функции, встроенные в ядро системы. При этом меняется их математический и физический смысл. Поэтому пользоваться пакетом надо с известной осторожностью. Для восстановления роли функций можно использовать команду restart.
Пакет VectorCalculus ориентирован в первую очередь на решение задач математической физики, использующих методы теории поля и приложения дифференциального исчисления. Он оперирует такими привычными для физиков (разумеется, и для математиков) понятиями, как поток векторного поля, градиент, тор-сион, векторный потенциал и др. Приведенный ниже материал поясняет применение большинства функций этого пакета. Полезно просмотреть и файл VectorCalculus.mws, содержащий примеры его применения. В Интернете можно найти целую серию уроков по векторному анализу и теории поля в виде пакета Calculus IV или V (разработчик проф. J. Wagner).
4.11.2. Объекты векторных вычислений
Вектор в геометрическом представлении в данном пакете по умолчанию задается в прямоугольной системе координат:
> v := Vector( [x,y,z]);
Здесь е х , е у и е z — проекции единичного вектора ена оси координат х, у и z. Тип координатной системы (по умолчанию — прямоугольная) можно определить следующим образом:
> attributes(v);
Для создания векторного поля служит функция
VectorField(v, с)
где v — вектор и с — опционально заданный параметр в форме name[name, name,...], задающий тип координатной системы.
Можно изменить систему координат, например, задав (с помощью функции установки координат SetCoordinates) полярную систему координат:
> SetCoordinates(polar);
> w := ;
> attributes(w);
Аналогично можно задать вектор в сферической системе координат:
> SetCoordinates(spherical[r,phi,theta]);
> F := VectorField();
> attributes(F);
Можно также сменить формат представления вектора и выполнить с ним некоторые простейшие векторные операции:
> BasisForrnat(false);
> v := ;
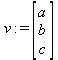
> BasisFormat(true);
> v;
> SetCoordinates(polar);
> MapToBasis(, 'cartesian');
> SetCoordinates(spherical);
> MapToBasis(, 'cartesian');
> SetCoordinates(spherical[r,phi,theta]);
> MapToBasis(VectorField(), 'cartesian'[x,y,z]);
Пакет VectorCalculus предусматривает возможность задания новой системы координат с помощью команды:
AddCoordinates(newsys, eqns, owrite)
где newsys — спецификация новой системы координат в виде symbol[name, name, …]; eqns — соотношения между координатами новой системы и прямоугольной системы координат, представленные в виде list(algebraic); owrite — заданное опционально равенство.
4.11.3. Основные операции с векторами
В данном пакете переопределены некоторые основные операции над векторами. Прежде всего, это операции сложения (+) и скалярного умножения (*), которые поясняются следующими примерами (файл vop) :
Читать дальшеИнтервал:
Закладка:










