Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Приведем еще несколько примеров использования функции Interp:
> Interp([2,5,6], [9,8,3], х) mod 11;
> alias(alpha=RootOf(х^4+х+1));
> a := Interp([0,1,alpha],[alpha,alpha^2,alpha^3], x) mod 2;
5.8. Применение числовой аппроксимации функций
5.8.1. Состав пакета numapprox
Для более глубоких и продвинутых операций аппроксимации служит специальный пакет расширения numapprox. Этот пакет содержит небольшое число безусловно очень важных функций:
> with(numapprox);
В их числе функции интерполяции и аппроксимации полиномами Чебышева, рядом Тейлора, отношением полиномов (аппроксимация Паде) и др. Все они широко применяются не только в фундаментальной математике, но и при решении многих прикладных задач. Рассмотрим их, начиная с функций аппроксимации аналитических зависимостей.
5.8.2. Разложение функции в ряд Лорана
Для разложения функции f в ряд Лорана с порядком n в окрестности точки x=а (или x=0) служит функция laurent:
laurent(f, х=а, n)
laurent(f, x, n)
Представленный ниже пример иллюстрирует реализацию разложения в ряд Лорана:
> laurent(f(х),х=0,4);
> laurent(exp(х),х,5);
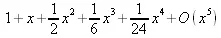
5.8.3. Паде-аппроксимация аналитических функций
Для аппроксимации аналитических функций одной из лучших является Паде-аппроксимация, при которой заданная функция приближается отношением двух полиномов. Эта аппроксимация способна приблизить даже точки разрыва исходной функции с устремлениями ее значений в бесконечность (при нулях полинома знаменателя. Для осуществления такой аппроксимации используется функция pade:
pade(f, х=а, [m,n])
pade(f, х, [m,n])
Здесь f — аналитическое выражение или функция, x — переменная, относительно которой записывается аппроксимирующая функция, a — координата точки, относительно которой выполняется аппроксимация, m, n — максимальные степени полиномов числителя и знаменателя. Технику аппроксимации Паде непрерывной функции поясняет рис. 5.17.
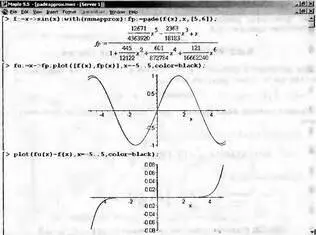
Рис. 5.17. Аппроксимация Паде для синусоидальной функции
На рис. 5.17 представлена аппроксимация синусоидальной функции, а также построены графики этой функции и аппроксимирующей функции. Под ними дан также график абсолютной погрешности для этого вида аппроксимации. Нетрудно заметить, что уже в интервале [-π, π] погрешность резко возрастает на концах интервала аппроксимации.
Важным достоинством Паде-аппроксимации является возможность довольно точного приближения разрывных функций. Это связано с тем, что нули знаменателя у аппроксимирующего выражения способны приближать разрывы функций, если на заданном интервале аппроксимации число разрывов конечно. На рис. 5.18 представлен пример Паде-аппроксимации функции tan(x) в интервале от -4,5 до 4,5, включающем два разрыва функции.
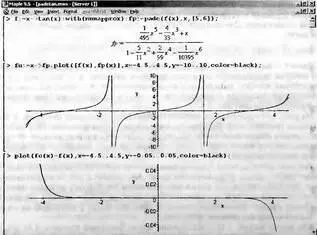
Рис. 5.18. Аппроксимация Паде для разрывной функции тангенса
Как видно из рис. 5.18, расхождение между функцией тангенса и ее аппроксимирующей функцией едва заметны лишь на краях интервала аппроксимации. Оба разрыва прекрасно приближаются аппроксимирующей функцией и никакого выброса погрешности в точках разрыва нет. Такой характер аппроксимации подтверждается и графиком погрешности, которая лишь на концах интервала аппроксимации [-4.0, 4.0] достигает значений 0,01 (около 1%).
5.8.4. Паде-аппроксимация с полиномами Чебышева
Для многих аналитических зависимостей хорошие результаты дает аппроксимация полиномами Чебышева. При ней более оптимальным является выбор узлов аппроксимации, что ведет к уменьшению погрешности аппроксимации.
В общем случае применяется Паде-аппроксимация, характерная представлением аппроксимирующей функции в виде отношения полиномов Чебышева. Она реализуется функциями chebpade:
chebpade(f, x=a..b, [m,n])
chebpade(f, x, [m,n])
chebpade(f, a..b, [m,n])
Здесь a..b задает отрезок аппроксимации, m и n — максимальные степени числителя и знаменателя полиномов Чебышева. Приведенный ниже пример показывает аппроксимацию Паде полиномами Чебышева для функции f=cos(x):
> Digits:=10:chebpade(cos(x),x=0..1,5);
> chebpade(cos(x),x=0..1,[2,3]);
5.8.5. Наилучшая минимаксная аппроксимация
Минимаксная аппроксимация отличается от Паде-аппроксимации минимизацией максимальной абсолютной погрешности во всем интервале аппроксимации. Она использует алгоритм Ремеза (см. ниже) и реализуется следующей функцией:
minimax(f, x=a..b, [m,n], w, 'maxerror')
minimax(f, a..b, [m,n], w, 'maxerror')
Здесь, помимо уже отмеченных параметров, w — процедура или выражение, maxerror — переменная, которой приписывается значение minimax-нормы. Ниже дан пример аппроксимации функции cos(x) в интервале [-3, 3]:
> minimax(cos(х),х=-3..3,[2,3],1,'minmax');
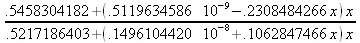
> minimax;
5.8.6. Наилучшая минимаксная аппроксимация по алгоритму Ремеза
Для получения наилучшей полиномиальной аппроксимации используется алгоритм Ремеза, который реализует следующая функция:
remez(w, f, a, b, m, n, crit, 'maxerror')
Здесь w — процедура, представляющая функцию w(x) > 0 в интервале [a, b], f — процедура, представляющая аппроксимируемую функцию f(х), а и b — числа, задающие интервал аппроксимации [a, b], m и n — степени числителя и знаменателя аппроксимирующей функции, crit — массив, индексированный от 1 до m + n + 2 и представляющий набор оценок в критических точках (то есть точек максимума/минимума кривых погрешности), maxerror — имя переменной, которой присваивается минимаксная норма w abs(f-r).
Читать дальшеИнтервал:
Закладка:










