Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Теперь рассмотрим еще более точную рациональную аппроксимацию Чебышева-Паде. Это такая рациональная функция r[m, n](х) с числителем степени m и знаменателем степени n такой же, как и для разложения в ряд Чебышева. Функция r[m, n](х) согласуется с разложения в ряд ряда Чебышева f(x) членом степени m+n. Мы вычислим аппроксимацию Чебышева-Паде степени (4, 4), подобную обычной Паде-аппроксимации, успешно выполненной ранее:

> ChebPadeApprox := chebpade(F, 0..4, [4,4]);

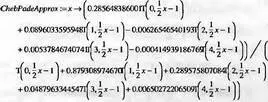
Построим кривую ошибок:

> with(orthopoly, Т):

> plot(F - ChebPadeApprox, 0..4,color=black);

Она представлена на рис. 5.27.

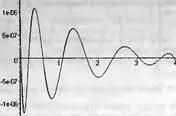
Рис. 5.27. Кривая ошибки при Паде-Чебышева рациональной аппроксимации

Максимальная ошибка и на этот раз имеет место в левой оконечной точке. Величина максимальной ошибки несколько меньше, чем ошибка при аппроксимации рядом Чебышева. Главное преимущество преставления в виде рациональной функции — высокая эффективность вычислений, которая может быть достигнута преобразованием в непрерывную (цепную) дробь (см. ниже). Однако полученная максимальная ошибка чуть-чуть больше заданной:

> maxChebPadeError := abs(F(0) - ChebPadeApprox(0));

Мы достигли впечатляющего успеха и остается сделать еще один шаг в направлении повышения точности аппроксимации.

Классический результат теории аппроксимации заключается в том, что минимакс как наилучшая аппроксимация рациональной функции степени (m, n) достигается, когда кривая ошибки имеет m+n+2 равных по величине колебаний. Кривая ошибки аппроксимации Чебышева-Паде имеет нужное число колебаний, но эта кривая должна быть выровнена (по амплитуде выбросов кривой ошибки) с тем, чтобы обеспечить наилучшее минимаксное приближение. Эта задача решается с помощью функции minimax:

> MinimaxApprox := minimax(F, 0..4, [4,4], 1, 'maxerror');

Максимальная ошибка в аппроксимации MinimaxApprox дается значением переменной maxerror. Заметим, что мы, наконец, достигли нашей цели получения аппроксимации с ошибкой меньшей, чем 1*10 -6:

> maxMinimaxError := maxerror;

Построим график погрешности для данного типа аппроксимации:

> plot(F - MinimaxApprox,0..4,color=black);

График ошибки, представленный на рис. 5.28 показывает равные по амплитуде колебания.

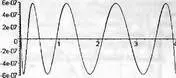
Рис. 5.28. График ошибки при минимаксной аппроксимации

Таким образом, мы блестяще добились успеха в снижении погрешности до требуемого и довольно жесткого уровня. Если бы мы задались целью получить только четыре или пять точных знаков аппроксимации, что в целом ряде случаев вполне приемлемо, то могли бы получить нужный результат гораздо раньше. Нам остается оптимизировать полученную аппроксимацию по минимуму арифметических операций и проверить реальный выигрыш по времени вычислений.

Полиномы числителя и знаменателя в минимаксной аппроксимации уже выражены в форме Горнера (то есть в форме вложенного умножения). Оценка полиномом степени n в форме Горнера при n умножениях и n суммированиях это наиболее эффективная схема оценки для полинома в общей форме. Однако, для рациональной функции степени ( m, n ) мы можем делать кое-что даже лучше, чем просто представить выражения числителя и знаменателя в форме Горнера. Так, мы можем нормализовать рациональную функцию так, что полином знаменателя со старшим коэффициентом будет равным 1. Мы можем также заметить, что вычисление рациональной функции степени (m, n) в форме Горнера требует выполнения всего m+n сложений, m+n-1 умножений и 1 деления. Другими словами, общий индекс действия есть

m + n операций умножения/деления,

m + n операций сложения/вычитания.

Вычисление рациональной функции можно значительно сократить и далее, преобразуя ее в непрерывную (цепную) дробь. Действительно, рациональная функция степени (m, n) может быть вычислена, используя только

max(m, n) операций умножения/деления,

m + n операций сложения/вычитания.

Например, если m = n, тогда эта новая схема требует выполнения только половины числа действий умножения/деления по сравнению с предшествующим методом. Для рациональной функции MinimaxApprox, вычисление в форме, выраженной выше, сводится к 9 действиям умножения/деления и 8 действиям сложения/вычитания. Число операций умножения/деления можно сократить до 8, нормализуя знаменатель к форме monic. Мы можем теперь вычислить непрерывную (цепную) дробь для той же самой рациональной функции. Вычисление по этой схеме, как это можно видеть из вывода Maple, сводятся только 4 действиям деления и 8 действиям сложения/вычитания:

> MinimaxApprox := confracform(MinimaxApprox):

> lprint(MinimaxApprox(x));

-.468860043555e-1 + 1.07858988373/

(x+4.41994160718+16.1901836591/(x+4.29118998064+70.1943521765/(x-10.2912531257+4.77538954280/(x+1.23883810079))))

Теперь определим время, необходимое для вычисления функции f(x) в 1000 точек, используя первоначальное интегральное определение, и сравним его с временем, требующимся для схемы MinimaxApprox в виде непрерывной дроби. Сделаем это для системы Maple 8. Так как наше приближение будет давать только 6 точных цифр, мы также потребуем 6 точных цифр и от интегрального представления функции:

> Digits := 6: st := time():

> seq( evalf(f(i/250.0) ) , i = 1..1000 ):

> oldtime := time() - st;

В процессе вычислений с использованием представления рациональной функции в виде непрерывной дроби иногда требуется внести несколько дополнительных цифр точности для страховки. В данном случае достаточно внести две дополнительные цифры. Итак, новое время вычислений:

> Digits := 6: st := time():

> seq( MinimaxApprox(i/250.0), i = 1..1000 ):

> newtime := time() - st;

Ускорение вычисления при аппроксимации есть:

> SpeedUp := oldtime/newtime;

Мы видим, что процедура вычислений, основанная на MinimaxApprox, выполняется почти в 12 раз быстрее процедуры с использованием исходного интегрального определения. Это серьезный успех, полностью оправдывающий время, потерянное на предварительные эксперименты по аппроксимации и ее оптимизации!