Луис Арталь - Том 19. Ипотека и уравнения. Математика в экономике

Чаще используются так называемые аннуитетные платежи. Размер аннуитетных платежей (как правило, выплачиваемых в конце расчетного периода) фиксирован. Часть аннуитетного платежа идет в уплату процентов, часть — в уплату основного долга по кредиту. В первые годы большую часть аннуитетных платежей составляют проценты и лишь малая часть идет в уплату долга по кредиту. С течением времени доля выплачиваемых процентов в каждом платеже уменьшается, а доля, идущая в уплату основного долга, возрастает. Чтобы рассчитать размер аннуитетного платежа по кредиту в размере С 0с процентной ставкой i, выданному на nрасчетных периодов (лет), нужно использовать формулу суммы геометрической прогрессии.

Геометрическая прогрессия — это последовательность чисел, в которой каждое последующее число начиная со второго получается из предыдущего умножением его на определенное число r, которое называется знаменателем прогрессии. Так, последовательность чисел а 1, а 2, а 3, а 4…, а n-1, а n(индекс обозначает порядковый номер: первый член последовательности обозначается цифрой 1, последний — n) является геометрической прогрессией тогда, когда для данного знаменателя rвыполняется соотношение: а 2= а 1∙ r, а 3 = а 2∙ r, …, а n= а n-1∙ r, так, что r= а n/ а n-1. Выразив члены геометрической прогрессии через ау получим:

a 1= a 1

a 2= a 1∙ r

a 3= a 1∙ r 2

……

a n= a 1∙ r n-1

Сумма этой геометрической прогрессии S nравна:

S= а 1+ а 2+ а 3 + … + а n-1+ а n (1)

Если умножить обе части равенства (1) на знаменатель r, получим:

r∙ S n= r∙( а 1+ а 2+ а 3 + … + а n-1+ а n ) = r∙ а 1+ r∙ а 2 + r∙ а 3 + … + r∙ а n-1+ r∙ а n

r∙ S n= а 2 + а 3+ … + а n+ r∙а n (2)

(если мы умножим данный член прогрессии а i на знаменатель r,получим следующий член, а i+1, так как а i+1= r∙ а i).

Вычтя из равенства (2) равенство (1), то есть r∙ S n— S n, получим:

r∙ S n— S n= — а 1+ r∙а n; S n∙( r— 1) = r∙ a n— a 1,

откуда

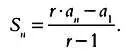
(3)

Это формула суммы геометрической прогрессии. Учитывая, что а n= a 1∙ r n-1и подставив это равенство в (3), имеем:

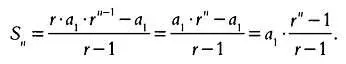
Вот еще одна форма записи суммы геометрической прогрессии:

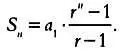
(4)

Для кредита с аннуитетным платежом а сроком nлет и процентной ставкой iбудущая стоимость капитала С n, выплаченная в виде суммы платежей аза nрасчетных периодов, будет равна:

С n = a∙ (1+ i) 0+ a∙ (1+ i) 1 +… + a∙ (1+ i) n-2 + a∙ (1+ i) n-1 = a+ a∙ (1+ i) 1+ … + a∙ (1+ i) n-2+ a∙ (1+ i) n-1

Результат является суммой геометрической прогрессии, первый член которой равен а, знаменатель — (1 + i).

Применив формулу (4) суммы геометрической прогрессии, получим

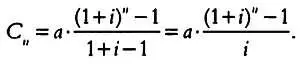
(5)

Учитывая, что С n= C 0∙(1+ i) n, и подставив это значение в (3), имеем:

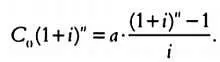
Перенеся переменную а, обозначающую сумму аннуитетного платежа, в левую часть, получим формулу для расчета суммы аннуитетного платежа по кредиту:

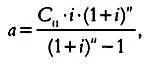
(6)

где С 0 — сумма кредита.

* * *

ПОСЛЕДОВАТЕЛЬНОСТИ

Геометрическая прогрессия — одна из простейших последовательностей, то есть это упорядоченное множество чисел, значение определенного члена которого можно вычислить с помощью математической формулы с переменной, указывающей место этого члена в последовательности.

Указанная формула задает общий член последовательности. Как правило, это функция а n= f(n), где n— порядковый номер члена последовательности.

Существуют другие последовательности, члены которых можно вычислить с помощью формулы, в которой фигурируют один или несколько предшествующих членов: например, последовательность Фибоначчи 1, 1, 2, 3, 5, 8, 13 в которой каждый член является суммой двух предыду щих, или последовательность, общий член которой выражается формулой а n= n + а n-1; a 1= 3 (членами этой последовательности являются 3, 5, 8, 12, 17, 23…).

В каждой последовательности необходимо указывать значение начального члена (или членов) и их количество (если последовательность является ограниченной). Если последовательность содержит бесконечное число членов, ее можно продолжать сколь угодно долго, вычисляя значения новых членов по формуле общего члена. Существуют возрастающие последовательности (значения их членов последовательно увеличиваются) и убывающие (значения их членов последовательно уменьшаются), которые могут быть ограниченными или неограниченными.

Последовательности широко используются в финансовой математике. Например, последовательность, члены которой обозначают сумму простых процентов, которые должны быть уплачены ежегодно при начальном капитале, равном 1, и процентной ставке, равной 20 %, выглядит так: 1; 1,2; 1,4; 1,6; 1,8; 2,0; 2,2;… Это неограниченная возрастающая последовательность, общий член которой выражается формулой a n= 1+ 0,2∙ n.

Последовательность, члены которой обозначают сумму сложных процентов, которые должны быть уплачены ежегодно при начальном капитале, равном 1, и процентной ставке, равной 20 %, выглядит так: 1; 1,2 2; 1,2 3; 1,2 4;… Это неограниченная возрастающая последовательность, общий член которой выражается формулой а n= (1+ 0,2) n.