Луис Арталь - Том 19. Ипотека и уравнения. Математика в экономике

x= v 1+ 2v 2

* * *

ФУНКЦИИ

Функция — это количественная взаимосвязь между переменными. В простейшем случае функция определяет влияние одной переменной — аргумента (ее значения выбираются произвольно) на другую переменную — зависимую (ее значение зависит от выбранного значения аргумента).

Существуют эмпирические функции, значения переменных для которых получены в результате эксперимента, и математические функции, в которых значения переменных подчиняются определенной формуле.

В экономике некоторые эмпирически выведенные зависимости между переменными можно приближенно описать математической функцией с помощью метода, называемого регрессией.

В других случаях используется формула, которая достаточно точно описывает связь между значениями двух переменных. Если мы будем рассматривать сумму, подлежащую уплате, как зависимую переменную, а число купленных единиц товара — как аргумент, то зависимость между ними будет определяться следующей формулой:

Сумма к уплате = стоимость за единицу товара ∙ число единиц товара.

В математической нотации эта функция будет записываться как f(x)= а∙ х, где f(x)обозначает, что значение f(зависимой переменной) зависит от х, а— постоянная, равная стоимости единицы товара, х— число приобретенных единиц товара (аргумент).

Математическую функцию можно представить тремя способами: в виде формулы, таблицы значений или графика в декартовой системе координат. Существует множество видов функций.

Простейшими являются линейные функции, или полиномы (многочлены) первой степени, как, например, f(х)= 0,65 х. Далее эта функция представлена в трех различных вариантах.

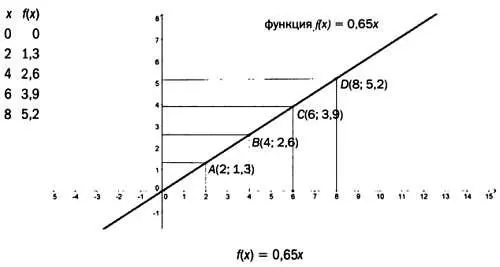
Функция f(x)= 0,65 х— это линейная возрастающая функция, или прямая пропорциональность.

С увеличением независимой переменной хзависимая переменная f(x)также возрастает. В случае с функцией, предложенной выше ( сумма к уплате = стоимость за единицу товара ∙ число единиц товара), число единиц товара не может принимать отрицательные значения, и часть графика, расположенная слева от 0, не имеет смысла. Существует множество других линейных функций.

Каждая из них описывает особый тип связи между двумя переменными — хи f(х), как, например, две убывающие линейные функции g(х)и h(х), графики которых представлены ниже.

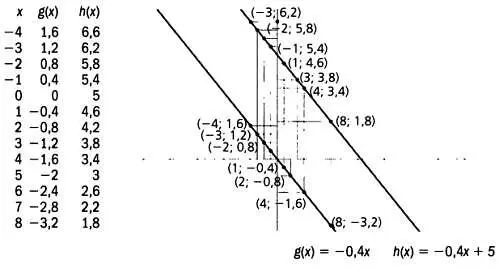
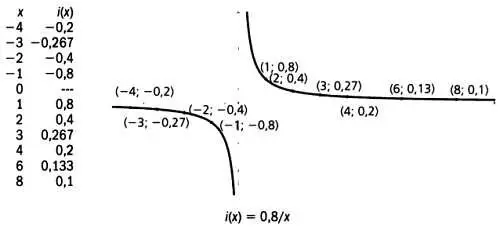
Функция i(х)называется обратной пропорциональностью. В функциях такого типа при возрастании независимой переменной хзначение зависимой переменной i(х)соответственно уменьшается. Например, когда хпринимает значение 3, i(х)равняется 0,8/3 = 0,267.

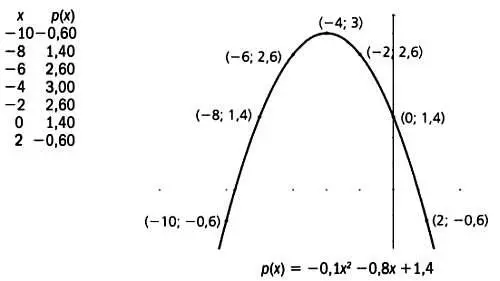
Также существуют полиномы второго порядка. Их графиками являются параболические кривые, как, например, график функции р(х), представленный на иллюстрации.

Периодические функции широко используются при решении многих задач биржевого анализа.

* * *

Для различных объемов производства сплава составляется следующая таблица производства. Числовые данные в таблице соответствуют формуле, которую мы привели выше.

Сочетание факторов производства при выпуске алюминиево-никелевого сплава.

Любое изменение технологий предполагает изменение сочетания факторов производства и, как следствие, ведет к формированию новой таблицы производства с последующим изменением производственной функции. Каждому состоянию технологий соответствует график производства с кривыми, описывающими, как объем готовой продукции связан со значениями всех факторов, соответствующих данному состоянию технологий. Так, например, на графике внизу слева можно увидеть изменение сочетания факторов производства v 1 и v 2соответствующих двум различным состояниям технологий Аи В.

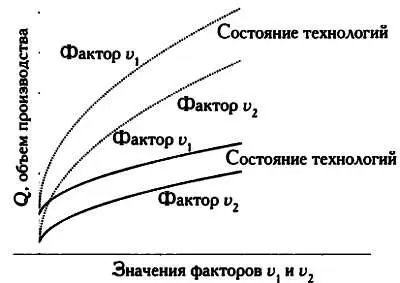
Кривые производительности.

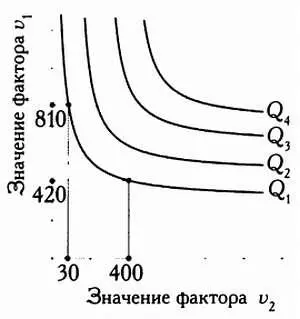
Изокванты (линии равного выпуска).

С применением различных технологий для выпуска одного и того же объема продукции (например, 50 кг сплава) будут использоваться разные сочетания факторов производства.

Графики, иллюстрирующие выпуск одного и того же объема готовой продукции Q 1(величины Q 1, Q 2, Q 3, Q 4на графике вверху справа), называются изоквантами — линиями равного выпуска.

Каждая изокванта иллюстрирует различные сочетания факторов производства, позволяющие получить один и тот же объем готовой продукции Q 1. Например, объем выпуска Qt можно обеспечить сочетанием 420 единиц фактора v 1и 400 единиц фактора v 2либо сочетанием 810 единиц фактора v 1и 30 единиц фактора v 2.

В процессе производства возникают постоянные и переменные издержки, зависящие от объема произведенной продукции. Сумма постоянных и переменных издержек равна общим издержкам. Предельные издержки определяются как дополнительные затраты, связанные с увеличением выпуска готовой продукции на одну единицу:

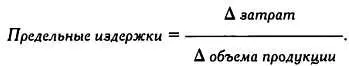
Предельные издержки также выражаются производной функции издержек по объему продукции:

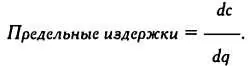
Для определенного объема выпуска значение производной равно тангенсу угла наклона касательной к кривой в точке А, соответствующей этому объему выпуска.

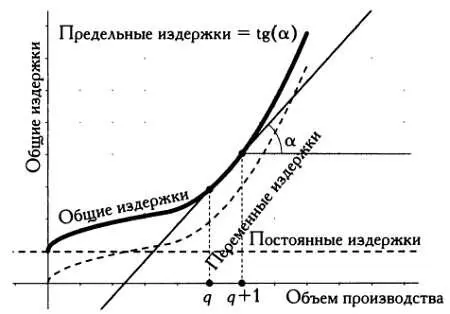
График общих издержек, производная функции издержек и касательная к графику.