Луис Арталь - Том 19. Ипотека и уравнения. Математика в экономике

Малый тренд сроком два дня.

* * *

Ральф Нельсон Эллиотт (1871–1948) позднее дополнил теорию Доу, описывающую поведение рынка ценных бумаг. Он заметил, что котировки изменяются в соответствии с определенными шаблонами. Эллиотт определил волны, по своему поведению схожие с числами Фибоначчи — числовым рядом, каждый член которого равен сумме двух предыдущих. В 1946 году, изучив значения промышленного индекса Доу-Джонса (DJIA), он изобразил эти волны на графике.

На основании полученного графика Эллиотт сделал вывод: в колебаниях цен прослеживаются повторяющиеся волны различной длительности и амплитуды колебаний. Волновой принцип Эллиотта гласит, что на рынках ценных бумаг наблюдается повторяющийся ритм: пять волн идут в направлении тренда, три волны — против тренда. Полный цикл состоит из восьми волн — пяти восходящих и трех нисходящих. В рамках цикла волны 1, 3 и 5 являются движущими (импульсными), 2 и 4 — коррекционными, они компенсируют эффект от волн 1 и 3. Пять восходящих волн сменяются тремя нисходящими, А, Ви С. В период снижения курсов акций на рынке также наблюдаются кривые, схожие с пятью волнами, описанными выше.

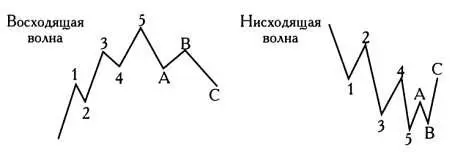
Как можно видеть, на графиках биржевых котировок реальных ценных бумаг действительно можно заметить волны Эллиотта.

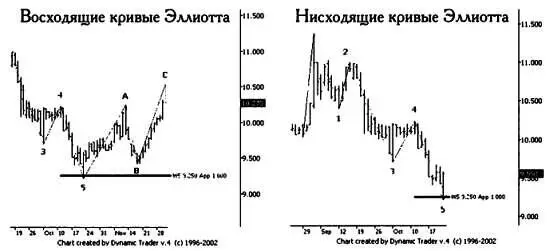
Если рассматривать волны Эллиотта как отражение психологии поведения участников рынка, которое вызывает значительные колебания биржевых котировок, то вполне логично предположить, что эти волны можно описать именно числами Фибоначчи.

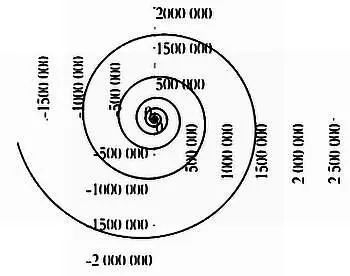
Эллиотт утверждал, что для описания рынков ценных бумаг применимо и золотое сечение. Таким образом, изменение котировок подобно логарифмической спирали, по форме напоминающей раковину улитки или облако в урагане. Говоря проще, можно предсказать, что по окончании периода роста наступит период снижения, длительность и амплитуда которого будут составлять 3/5 длительности и амплитуды периода роста.

Было отмечено, что изменение цен на основные товары также описывается волнами Эллиотта, — это можно заметить на примере такого товара, как золото: в последнее время его цена неизменно движется в направлении, противоположном биржевому тренду, следовательно, оно также следует волнам Эллиотта, но в противоположном направлении.

* * *

ЧИСЛА ФИБОНАЧЧИ И БИРЖА

Изучив изменения котировок на многих рынках ценных бумаг, Эллиотт определил, что в основе теории волн лежит последовательность Фибоначчи, открытая еще в XIII веке! Эта последовательность (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 …) обладает многими свойствами, применимыми к биржевому анализу.

Сумма любых двух соседних членов последовательности равна ее следующему члену, отношение любого члена последовательности к следующему стремится к иррациональному числу Ф — 1–0,618034 … (где Ф— так называемое золотое число, описывающее золотое сечение), которое часто встречается в природе и произведениях искусства. Таким образом, когда коррекционная волна достигает 61,8 % прежней величины индекса, наступает поворотный момент: рыночный тренд либо сменится на противоположный, либо сохранит направление, и индекс достигнет 100 % от прежнего значения.

Квадратные корни, которые не являются целыми или рациональными числами, относятся к новому, отдельному классу так называемых иррациональных чисел, которые нельзя представить в виде дроби. Эти числа содержат бесконечное множество десятичных знаков и, в отличие от рациональных чисел, в их записи отсутствуют циклы, или периоды, как, например,

4/7 = 0,571428571428571428571…

Примерами иррациональных чисел являются число π, число е, используемое при расчете сложных процентов, и золотое число Ф.

При эмиссии государственных облигаций покупатель совершает начальные вложения, а затем в течение срока действия облигации получает доход. Чтобы вычислить общую рентабельность за весь срок владения облигацией, рассчитывается внутренняя норма доходности, причем в качестве доходов учитываются и налоговые вычеты.

При эмиссии облигаций с переменной процентной ставкой общая рентабельность обычно рассчитывается по формуле чистого дисконтированного дохода на основе примерной цены денег (процентной ставки). Этот же метод используется для оценки прибыльности предприятия, когда денежные потоки за каждый год приводятся к текущему моменту времени с учетом объема начальных вложений и определенной ставки дисконтирования.

Рассмотрим расчет годовой рентабельности инвестиций. В момент времени tбыла совершена инвестиция в размере I 0, по прошествии nдней акции были проданы за I t, причем I 0< I t. Общий доход В в результате инвестирования равен разнице курсов акций | I t— I 0| > 0 вкупе с дивидендами, правом подписки на акции и т. д.

Рентабельность инвестиций R(в %) будет равна:

R= (B/ I 0)∙ 100

Рентабельность за год R aрассчитывается по правилу пропорции:

рентабельность Rза срок в ___ nдней

рентабельность Rза срок в ___ 365 дней

R a= R∙ (365/ n)

Часто при оценке доходности ценных бумаг используется показатель PER (коэффициент цена/прибыль), который связывает цену приобретения бумаги С t с полученными или ожидаемыми доходами от нее за период t(дивиденды, ожидаемая положительная курсовая разница и т. д.):

PER= C t/ G t = Цена акции/ Чистая прибыль (на акцию)

где C t— стоимость бумаги, G t— ожидаемая прибыль от нее за период t.

Обратите внимание, что показателем, обратным этому коэффициенту, является рентабельность акции:

Рентабельность акции= Чистая прибыль (на акцию)/ Цена акции= 1/ PER

Чаще всего используются следующие коэффициенты, показывающие финансовые итоги в пересчете на акцию:

Дивидендная доходность = Общие дивиденды/ Рыночная капитализация= Дивиденд на одну акцию/ Курс акции