Луис Арталь - Том 19. Ипотека и уравнения. Математика в экономике

где

Дивиденд на акцию= Прибыль после уплаты налогов/ Количество акций

если прибыль после уплаты налогов полностью распределяется между акционерами.

Если же в виде дивидендов выплачивается лишь часть прибыли, то важен коэффициент, показывающий, какая именно доля прибыли направлена на уплату дивидендов.

Дивиденды могут рассчитываться на основе учетной стоимости акций, их рыночной или номинальной стоимости.

Коэффициент, связывающий денежный поток предприятия ( чистый доход = прибыль + амортизация ) с числом акций:

Денежный поток на акцию= (Прибыль+ амортизация)/ Количество акций

Индикатор βпоказывает уровень риска, связанный с вложением в определенные ценные бумаги, и характеризует волатильность котировок ценной бумаги. Если коэффициент βравен n, это означает, что доходность волатильной ценной бумаги в n раз больше доходности по индексу или по всем ценным бумагам на рынке. Так, если β= 2, а средняя доходность ценных бумаг на рынке равна 10 %, то доходность рассматриваемой ценной бумаги составит 20 %.

Риск измеряется путем сравнения доходности ценной бумаги и всех бумаг на рынке, при этом ее доходность будет отклоняться от среднерыночной. Эти отклонения оцениваются с помощью среднеквадратического отклонения σ или дисперсии, равной σ 2. Если средняя доходность по рынку равна R, а доходность ценной бумаги iравна R i, то риск, рассчитанный с помощью среднеквадратического отклонения, будет равен:

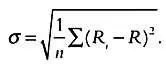
Также можно использовать полудисперсию, то есть дисперсию, в которой учитываются только отрицательные отклонения, характеризующие риск потери средств.

В экономике часто существует взаимосвязь между произвольными переменными — ковариация. Считается, что между двумя статистическими переменными существует ковариация, если между ними наблюдается однонаправленная причинно-следственная связь (значения переменной Xвлияют на значения Y, но не наоборот) или взаимозависимость (значения Xвлияют на значения Yи наоборот).

Изучение ковариации между двумя статистическими переменными можно начать с графических методов. На следующих диаграммах представлено множество точек, соответствующих парам значений переменных, для которых мы хотим определить наличие ковариации. Эта диаграмма называется диаграммой рассеяния.

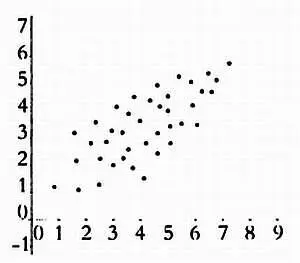
Положительная линейная корреляция.

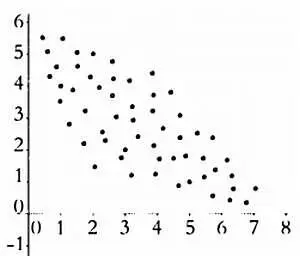
Отрицательная линейная корреляция.

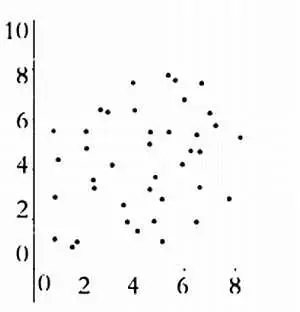
Отсутствие корреляции.

Существуют два метода анализа ковариации между двумя статистическими переменными: регрессия и корреляция. При анализе корреляции рассчитывается числовой коэффициент, который используется как индикатор степени ковариации между двумя переменными, а при регрессионном анализе определяется математическая функция, описывающая ковариацию для всех значений переменных.

Вывод коэффициента корреляции для всей генеральной совокупности на основе анализа выборки, который обозначается R, выполняется на основе коэффициента корреляции r, рассчитанного для выборки. Этот процесс подробно изучен. По сути, r можно рассмотреть как оценочное значение Rи проанализировать, действительно ли оно является точным оценочным значением. Выборки из одной и той же генеральной совокупности можно формировать множеством способов, и коэффициент корреляции на каждой выборке будет отличаться. Коэффициенты корреляции rдля всех возможных выборок являются значениями случайной величины, которая характеризуется собственным распределением.

* * *

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

Чтобы подтвердить исходное предположение, что между двумя переменными наблюдается корреляция (к такому выводу можно прийти, взглянув на диаграмму рассеяния), рассчитаем коэффициент корреляции. Для выборки из nпар значений ( х i, у i) при i= 1, 2, 3…., nпоказателем линейной связи между переменными является r — линейный коэффициент корреляции,

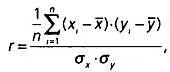
где х ¯, у ¯, σ х, σ у— средние значения и среднеквадратические отклонения, рассчитанные для переменных Xи Yна выборке. Значения коэффициента корреляции rвсегда находятся в интервале от -1 до 1. Если r= 1 или r = -1, то все точки, соответствующие выборке, лежат на одной прямой. Если значение rблизко к 1 (или к -1), то между двумя переменными имеется очень сильная линейная зависимость. Если значение r мало (близко к 0), то зависимость между двумя переменными практически отсутствует, за исключением случаев, когда на основе диаграммы рассеяния можно сделать вывод о наличии нелинейной корреляции.

Коэффициент r— безразмерная величина, не зависящая от единиц измерения значений X и Y.

В следующей таблице представлены значения двух статистических переменных, Xи Y, на выборке объемом в пять значений

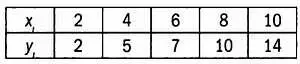
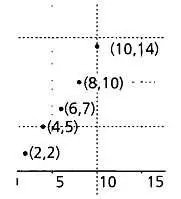
Диаграмма рассеяния.

Для анализа корреляции рассчитывается среднее х, среднеквадратическое отклонение σи коэффициент r.

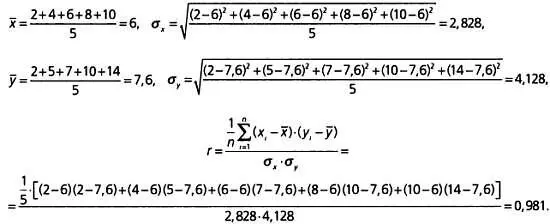
ЛИНИИ РЕГРЕССИИ

Если точки ( х, у) на диаграмме рассеяния расположены близко к некоторой прямой или кривой, то можно определить функцию, которая с наибольшей точностью будет описывать это множество точек. Графиком указанной функции будет линия регрессии, которую можно будет использовать для составления прогнозов.

Математический метод, используемый для определения функции, которая точнее всего описывает множество значений выборки, называется методом наименьших квадратов.