Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Запутанная история золотого сечения началась в VI веке до нашей эры и дошла до сегодняшнего дня. Эти двадцать шесть столетий пронизаны двумя основными нитями повествования. Я имею в виду, с одной стороны, пифагорейский девиз «Все есть число», который поразительным образом воплощается в действительность в самом буквальном смысле – в той роли, которую играет золотое сечение в природе, от филлотаксиса до формы галактик, – а с другой стороны, пифагорейскую одержимость символическим значением правильного пятиугольника, которая преобразилась в ложное, по моему мнению, представление, что золотое сечение – это универсальной канон идеала красоты. После всего этого читатель вправе задаться вопросом, стоит ли и дальше исследовать это простое, на первый взгляд, правило разделения отрезка.

Голландский художник Ян Вермеер (1632–1675) знаменит своими поразительными, чарующими жанровыми полотнами, на которых, как правило, изображены один-два человека за повседневными делами. На многих этих картинах слева от зрителя расположено окно, которое освещает комнату мягким светом, и отражение этого света от плиток на полу оставляет впечатление подлинного волшебства. Если пристально рассматривать эти картины, окажется, что на многих из них – в частности, я имею в виду картины «Концерт», «Дама, пишущая письмо, со своей служанкой», «Любовное письмо» (рис. 92, хранится в Государственном музее в Амстердаме) и «Аллегория живописи» (рис. 93, хранится в Музее истории искусств в Вене) – изображен пол с одним и тем же плиточным узором из черных и белых квадратов.

Рис. 92

Рис. 93

Если хочешь получить покрыть плитками весь пол и получить при этом повторяющийся через равные промежутки узор, то мостить полы удобнее всего именно квадратами, равносторонними треугольниками и правильными шестиугольниками, и это называется «периодическое замощение» (рис. 94). Простые, ничем не украшенные квадратные плитки и узоры, которые они образуют, обладают четырехсторонней симметрией: если повернуть их на четверть круга, то есть на 90 градусов, они останутся прежними. Подобным же образом плитки в виде равносторонних треугольников обладают трехсторонней симметрией (они остаются прежними при повороте на треть круга, то есть на 120 градусов), а плитки в виде правильных шестиугольников – шестисторонней симметрией (то есть остаются прежними при повороте на шестую часть круга, на 60 градусов).

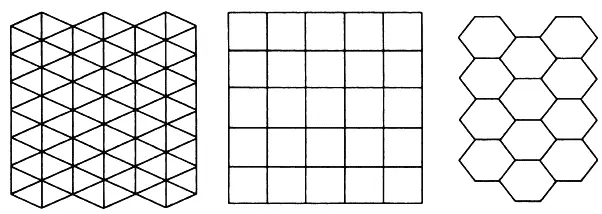
Рис. 94

Рис. 95

Однако периодические замощения возможны и при помощи более сложных геометрических фигур. Например, крепость Альгамбра в Гренаде, один из самых потрясающих памятников мусульманской архитектуры, отделана разнообразными сложными узорами из плиток (рис. 95). Некоторые из них даже вдохновили знаменитого голландского графика М. К. Эшера (1898–1972), и он создал множество весьма изысканных узоров-замощений (например, рис. 96), которые называл «разбиением плоскости».

Рис. 96

Теснее всего из всех геометрических фигур с золотым сечением связан, конечно, правильный пятиугольник, обладающий пятисторонней симметрией. Однако одними правильными пятиугольниками плоскость не замостишь, периодического узора не получится. Сколько ни старайся, останутся незаполненные промежутки. Поэтому долгое время считалось, что невозможно создать замощение с крупномасштабной упорядоченностью (так называемым «дальним порядком»), обладающее пятисторонней симметрией. Однако Роджер Пенроуз в 1974 году обнаружил два основных набора плиток, при помощи сочетания которых можно замостить плоскость целиком, соблюдая при этом «запретную» пятистороннюю симметрию. Получившиеся узоры не строго периодичны, хотя и обладают дальним порядком.

Мозаики Пенроуза, можно сказать, сплошь построены на золотом сечении. Одна из пар плиток, которые рассматривал Пенроуз, состоит из двух фигур под названием «дротик» и «змей» (рис. 97, a и b соответственно). Обратите внимание, что обе фигуры состоят из двух равнобедренных треугольников, входящих в состав правильного пятиугольника (рис. 25). Треугольник, у которого отношение стороны к основанию равно φ, – это так называемый золотой треугольник (рис. 97, b ), а треугольник, у которого отношение стороны к основанию равно 1/φ, – это золотой гномон (рис. 97, a ). Эти фигуры можно получить, если разделить в золотом сечении длинную диагональ ромба с углами 72 и 108 градусов (рис. 98).

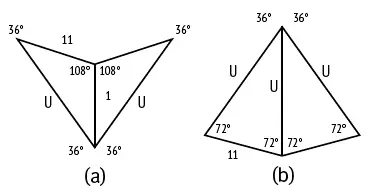
Рис. 97

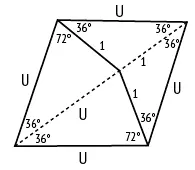
Рис. 98

Пенроуз и принстонский математик Джон Хортон Конвей показали, что для того, чтобы замостить плоскость змеями и дротиками непериодическим образом, как на рис. 99, нужно соблюдать определенные правила сочетаемости. Для этого удобно наносить на стороны фигур «метки» в виде выступов и пазов, как на кусочки паззла (рис. 100). Далее Пенроуз и Конвей доказали, что змеи и дротики могут непериодически заполнять плоскость бесконечным множеством способов, поскольку каждый узор можно окружить любым другим узором и таким образом создать третий, отличающийся от первых двух. Одно из самых поразительных свойств любой мозаики Пенроуза из дротиков и змеев состоит в том, что количество змеев примерно в 1,618 раз больше количества дротиков. То есть, если мы обозначим количество змеев как N змеев , а количество дротиков как N дротиков , то чем больше площадь, тем ближе отношение N змеев / N дротиков к числу φ.

Рис. 99