Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

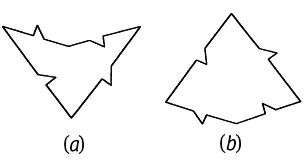
Рис. 100

Другая пара Пенроуза, непериодически заполняющая плоскость целиком, состоит из двух ромбов, «толстого» и «тонкого» (рис. 101). Как и пара «змей-дротик», каждый из ромбов состоит из двух золотых треугольников или двух золотых гномонов (рис. 102), и при замощении плоскости нужно соблюдать определенные правила сочетаемости, для удобства чего на нашем рисунке стороны и углы ромбов помечены и разрисованы (рис. 103), и тогда получается узор, заполняющий всю плоскость, как на рис. 4. Опять же «толстых» ромбов на замощение большой площади идет в 1,618 раз больше, чем «тонких», и N толстых / N тонких = φ. «Толстые» и «тонкие» ромбы теснейшим образом связаны со змеями и дротиками, а обе эти пары – посредством золотого сечения – с системой пятиугольника-пентаграммы.

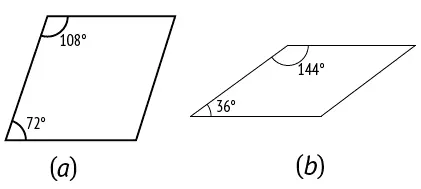
Рис. 101

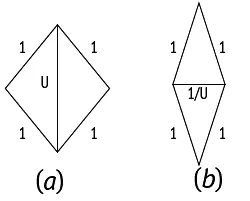
Рис. 102

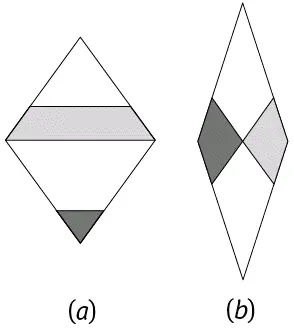
Рис. 103

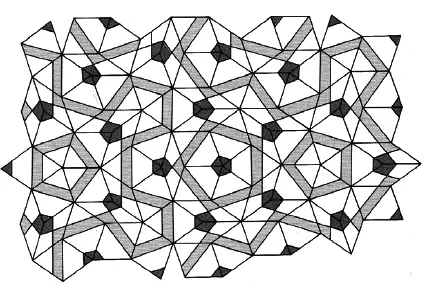
Рис. 104

Вспомним, что интерес пифагорейцев к золотому сечению начался с бесконечной череды вписанных друг в друга правильных пятиугольников и пентаграмм – как на рис. 105. На этом чертеже спрятаны все четыре плитки Пенроуза. Точки B и D отмечают противоположные дальние углы змея DCBA, а точки A и C – «крылышки» дротика EABC. Аналогичным образом можно найти на рисунке и «толстый» ромб AECD, и «тонкий» (в меньшем масштабе) ABCF.

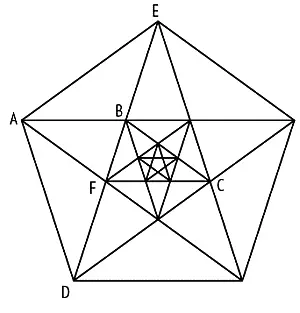
Рис. 105

Пенроуз продолжил изыскания в области мозаик и в трехмерном пространстве. Двумерные плитки замощают плоскость, а трехмерные «кирпичи» заполняют пространство. В 1976 году математик Роберт Амманн обнаружил пару «кирпичей» (рис. 106), «сплюснутый» и «растянутый», так называемые ромбоэдры, которыми можно заполнить пространство без промежутков. Более того, Амманн сумел доказать, что при наличии набора правил о сочетаемости граней получается непериодический узор, обладающий симметрическими свойствами икосаэдра (Рис. 20, e ; это эквивалент пятисторонней симметрии в трех измерениях, поскольку на каждой вершине сходятся пять симметричных ребер). Не стоит удивляться, что эти два ромбоэдра – это золотые ромбоэдры, и их грани идентичны ромбам в плитках Пенроуза (рис. 101).

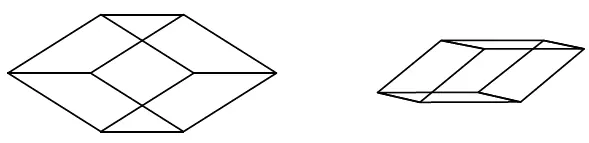
Рис. 106

Плитки Пенроуза так и держались бы в относительной тени, оставшись уделом занимательной математики, если бы не сенсационное открытие 1984 года. Израильский инженер, специалист по сопротивлению материалов Дан Шехтман с коллегами обнаружили, что кристаллы сплава марганца и алюминия обладают и дальним порядком, и пятисторонней симметрией. Это был настоящий переворот в кристаллографии: примерно такой же сенсацией для зоологов стало бы обнаружение стада пятиногих коров. Физики-твердотельщики и кристаллографы много десятков лет пребывали в убеждении, что твердые тела могут принимать лишь две основные формы – или полностью периодические кристаллы, структура которых строго упорядочена, или совершенно аморфные тела. В упорядоченных кристаллах, например, в привычной нам поваренной соли, атомы или группы атомов составляют узор, который в точности повторяется, и эти повторяющиеся узоры называются элементарными ячейками и формируют периодические структуры. Например, в случае соли элементарная ячейка – куб, каждый атом хлора окружен соседними атомами натрия и наоборот, каждый атом натрия оказывается окружен атомами хлора (рис. 107). Это очень похоже на идеально замощенный плитками пол: положение и ориентация каждой элементарной ячейки однозначным образом определяет общий узор. А в аморфных материалах, например, в стекле, атомы совершенно дезорганизованы. Считалось, что раз периодически замостить плоскость без промежутков могут только фигуры вроде квадратов – с четырехсторонней симметрией, – равносторонних треугольников – с трехсторонней симметрией, – и правильных шестиугольников – с шестисторонней симметрией, значит, в природе существуют исключительно кристаллы с двух-, трех-, четырех– и шестисторонней симметрией. Кристаллы Шехтмана вызвали совершеннейшую оторопь, поскольку обладали не просто строго упорядоченной структурой, как периодические кристаллы, но и пятисторонней (икосаэдральной) симметрией. До этого открытия мало кто подозревал, что возможно состояние материи, обладающее важными свойствами как кристаллических, так и аморфных субстанций. Новую разновидность кристаллов (после открытия Дана Шехтмана были найдены и другие сплавы алюминия) называют теперь квазикристаллами: они не аморфны, как стекло, но и не совсем периодичны, как соль. Иначе говоря, эти необычные материалы обладают теми же свойствами, что и мозаики Пенроуза! Однако от этого понимания как такового физикам нет особого толка: они хотят разобраться, как и почему формируются квазикристаллы. Правила сочетаемости Пенроуза и Амманна в данном случае не более чем хитроумное математическое упражнение, которое вовсе не объясняет поведения атомов или групп атомов в природе. В частности, трудно представить себе энергетическую конфигурацию, допускающую существование двух типов групп атомов (подобно двум ромбоэдрам Аммана) именно в той пропорции, которая обеспечивает наблюдаемую плотность.

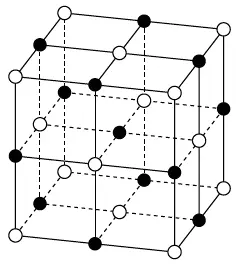
Рис. 107

Вероятное объяснение было найдено в 1991 году, когда математик Сергей Емельянович Бурков из Института теоретической физики им. Ландау в Москве обнаружил, что для квазипериодического замощения плоскости не обязательно нужны плитки двух видов. Бурков доказал, что квазипериодичности можно добиться даже при помощи одной плитки десятиугольной формы, если допустить, чтобы плитки перекрывались: такое свойство ранее не допускалось при замощениях плоскости. Пять лет спустя немецкий математик Петра Гуммельт из Университета имени Эрнста Морица Арндта в городе Грайфсвальд убедительно доказала, что мозаику Пенроуза можно получить при помощи одного «раскрашенного» десятиугольника в сочетании с конкретным правилом, допускающим перекрывание: два десятиугольника могут накладываться друг на друга, только если при этом перекрываются темные участки рисунка (рис. 108). Этот десятиугольник также имеет прямое отношение к золотому сечению: радиус круга, в который вписан правильный десятиугольник со стороной 1, равен φ.