Хавьер Фресан - Мир математики: m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

41

ВЕЙЛЬ: Присаживайтесь, господин Леви-Стросс.

ЛЕВИ-СТРОСС: Вы объясните мне, что такое группа?

ВЕЙЛЬ: Постараюсь. Мне хотелось бы начать с одного примера — он очень прост, но в нем постепенно раскрывается большинство основных понятий теории групп. Представьте себе равносторонний треугольник — надеюсь, вы помните, что это треугольник, все стороны которого равны. Меня интересуют движения, которые не меняют положение треугольника, то есть такие, когда сторонний наблюдатель не сможет увидеть разницу между треугольниками «до» и «после». Говорят, что треугольник инвариантен относительно таких преобразований.

ЛЕВИ-СТРОСС: Простите, я перебью вас, господин Вейль. Я кое-что не понял: если фигура в результате этих преобразований не меняется, то как определить, выполнили мы это преобразование или нет? Ведь треугольники не имеют памяти!

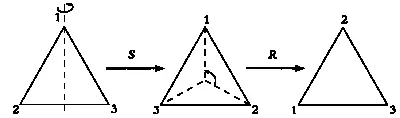
ВЕЙЛЬ: Хороший вопрос. Я как раз собирался ответить на него. Нужно пронумеровать вершины треугольника. Он будет выглядеть так же, однако в результате преобразования положение вершин изменится, таким образом, преобразование оставит свой след. Вершины нумеруются исключительно из соображений удобства.

Первая разновидность движения, которую мы рассмотрим, — поворот на 120° против часовой стрелки относительно центра треугольника.

Обозначим это преобразование через R. Как я уже говорил, увидеть результат R нельзя, но если мы бы, к примеру, пронумеровали вершины треугольника, начиная с верхней, против часовой стрелки, то можно было бы сказать, что R переводит первую вершину в третью, вторую — в первую, третью — во вторую. Проще всего показать это на рисунке.

43

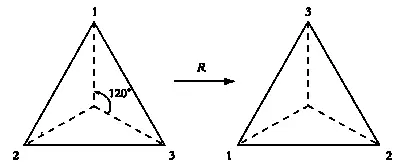
Результат поворота R.

Видите? Треугольник не изменился, но теперь его вершины пронумерованы 3—1—2, а не 1—2—3.

R не единственное преобразование, оставляющее треугольник неизменным.

Представьте себе осевую симметрию, ось которой пересекает треугольник. Чтобы в результате симметрии треугольник остался неизменным, нужно внимательно выбрать ось, так как при некоторых видах симметрии положение треугольника изменится.

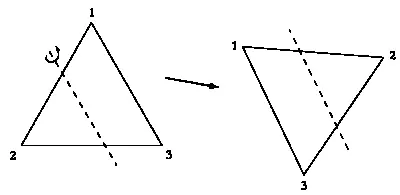
Симметрия, при которой треугольник меняется.

Треугольник останется неизменным, если ось симметрии проходит через его центр и одну из вершин. Поворот мы обозначили через R, симметрию — через S. Та же схема, которой мы проиллюстрировали поворот R, поможет показать, как изменится положение вершин при симметрии S. Первая вершина останется на месте, а вторая и третья поменяются местами. Теперь вершины пронумерованы не 1—2—3, а 1-3-2.

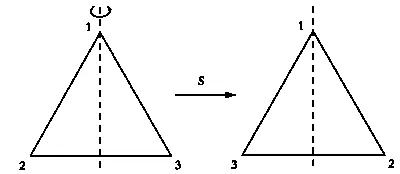
Результат симметрии S.

Теперь нам известны преобразования R и S. Что с ними можно сделать?

ЛЕВИ-СТРОСС: Выполнить сначала первое, а затем — второе?

ВЕЙЛЬ: Именно! Основное свойство этих преобразований заключается в том, что для двух таких преобразований можно определить их композицию. Применим поворот R, затем — симметрию S и обозначим полученный результат как SR. Мы привыкли читать слева направо, поэтому было бы логичнее записать RS, так как поворот R выполняется первым. Однако обозначение SR имеет свои преимущества.

Найдем композицию двух исходных преобразований.

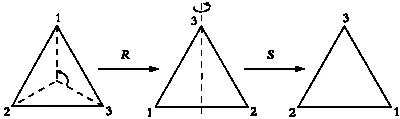
Композиция преобразований R и S.

На рисунке показано, что при движении SR вторая вершина остается неизменной, а две другие меняются местами. Следовательно, порядок следования вершин меняется с 1—2—3 на 3—2—1. Обратите внимание, что этот же результат можно

45

получить, применив к исходному треугольнику осевую симметрию, ось которой проходит через вторую вершину. Два этих преобразования совпадают.

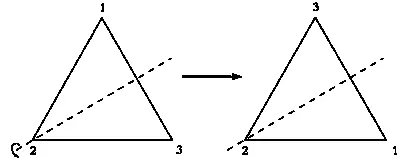
Композиция преобразований SR представляет собой симметрию.

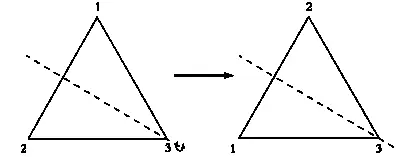
Теперь определим RS, то есть сначала применим S, а затем R, и посмотрим, как изменится порядок вершин.

ЛЕВИ-СТРОСС: Но от перемены мест множителей произведение не меняется.

ВЕЙЛЬ: Ах, эта юность, эта святая простота! Как же сложно по-новому посмотреть на то, что всем известно с детства. «От перемены мест множителей произведение не меняется» только при умножении чисел: трижды семь — то же, что и семью три. Однако нет никакой причины, по которой этот закон должен выполняться для других операций, например для сочетания движений, оставляющих исходную фигуру неизменной. Между прочим, это четко видно в нашем примере. Если сначала мы выполним S, а затем R, то получим...

Композиция преобразований S и R.

Вершины будут располагаться в порядке 2—1—3. Таким образом, результаты движений SR и RS отличаются.

46

ЛЕВИ-СТРОСС: Но RS — тоже симметрия.

Преобразование RS — симметрия.

ВЕЙЛЬ: Да, и ее ось проходит через третью вершину. Для того чтобы при симметрии треугольник оставался неизменным, ось симметрии должна проходить через его центр и одну из вершин. На основе R и S можно определить все возможные разновидности такой симметрии. Если ось симметрии проходит через вторую вершину, это симметрия SR, если через третью — RS. Добавив к ним собственно симметрию S, ось которой проходит через первую вершину, получим полный перечень:

S, SR и RS — все возможные виды симметрии, оставляющие треугольник неизменным.

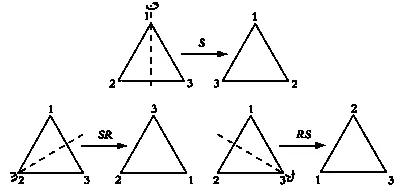
Виды симметрии, оставляющие треугольник неизменным.

ЛЕВИ-СТРОСС: Послушайте, господин Вейль, чтобы мы могли составить композицию двух преобразований, они обязательно должны отличаться?

47

ВЕЙЛЬ: Вовсе нет. Ничто не мешает применить одно и то же преобразование несколько раз подряд. Так как поворот фигуры два раза подряд на 120° равносилен повороту на 240°, движение RR также будет поворотом, при котором треугольник остается неизменным. Вместо RR будем записывать R 2. Если мы повернем фигуру еще на 120°, она совпадет с исходной. Таким образом, R3 никак не изменяет треугольник. Мы не учли преобразование, которое оставляет порядок следования вершин неизменным — 1—2—3. Будем называть это преобразование тождественным и обозначим его через I. Обратите внимание, что композицией тождественного преобразования и любого другого движения будет это движение.