Хавьер Фресан - Мир математики: m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

58

ЛЕВИ-СТРОСС: А для чего нужно это свойство?

ВЕЙЛЬ: Оно, в частности, позволяет доказать, что таблица умножения конечной группы — это латинский квадрат. Напомню: латинский квадрат — это таблица чисел, в каждой строке и в каждом столбце которой записаны все элементы группы.

Обозначим их через а 1а 2... а n. Приведем доказательство для второго столбца таблицы; для любого другого столбца оно будет аналогичным. Какие элементы записаны во втором столбце? Те, что определяются умножением а 2на все элементы группы, то есть а 2* а 1, а 2* a 2, а 2* а 3... и так далее до а 2* а n. Допустим, что два выражения из этого списка равны, то есть существуют два индекса j и k такие, что а 2* а j= а 2* a k. Так как а 2приводится в обеих частях выражения, по закону сокращения имеем а j= a k. Таким образом, в этом столбце нет двух одинаковых элементов!

Но так как группа состоит из n элементов, а в столбце таблицы нужно записать n неповторяющихся элементов, то в этом столбце будут записаны все элементы группы! Понимаете?

ЛЕВИ-СТРОСС: Для строк это свойство доказывается аналогично — достаточно поменять множители местами.

ВЕЙЛЬ: Вы определенно делаете успехи, господин Леви-Стросс. Мне кажется, вы готовы ко встрече с новыми группами. Помните, совсем недавно я говорил, что групповая операция на множестве из трех элементов определяется единственным образом? Теперь я объясню, почему это так, но прежде чем изучить случай с тремя элементами, рассмотрим группы порядка 1 и 2. Я уже объяснял, что такое порядок группы? По-моему, нет. Для конечных групп порядком называется число элементов группы.

ЛЕВИ-СТРОСС: Но мы уже дали порядку другое определение, не так ли?

ВЕЙЛЬ: И да, и нет. В примере с преобразованиями треугольника я говорил, что R имеет порядок, равный трем, так как три поворота фигуры на 120°, выполненные последовательно, не изменяют ее. В общем случае порядок элемента равен n, если, выполнив операцию над этим элементом n раз (или возведя его в степень n), мы получим тождество. Вам может показаться, что это определение не имеет ничего общего с предыдущим, но сейчас я продемонстрирую, что это не так.

Рассмотрим произвольный элемент группы, например а. Мы можем составить группу степеней а, то есть <���а> = {а, а 2, а 3...}, где а 2— сокращенное обозначение а * а, а 3обозначает а * а * а и так далее. Допустим, что а имеет порядок n в соответствии с первым определением, то есть а n— нейтральный элемент группы. Тогда перечень степеней остановится на а n= е и затем начнется сначала, так как

а n+1= а n* а = е*а = а, а n+2= а 2

и так далее. На самом деле множество будет содержать

59

всего n элементов: <���а> = {а, а 2... а n= е}. И это непростое множество: <���а>, в свою очередь, является группой: оно содержит нейтральный элемент, результат операции над двумя степенями а всегда равен степени а, и элемент а n-iявляется обратным для а i. Следовательно, порядок элемента — это порядок множества, состоящего из его степеней. Это новое определение носит более общий характер, чем первое.

Впрочем, интереснее другое. Я предлагаю вам поупражняться в различных действиях над группами и посмотреть, как выглядят группы наименьшего порядка.

В определении группы мы указали, что она обязательно должна содержать нейтральный элемент, поэтому группа не может быть пустой — она всегда будет содержать как минимум нейтральный элемент. Если порядок группы равен единице, она не может содержать других элементов, поэтому будет выглядеть так: G = {е}. Посмотрим, как выглядят группы из двух элементов. Они должны иметь вид G = {е, а}, где е — нейтральный элемент, а — другой элемент, отличный от е. По определению, а*е = е*а = а, а также е * е = е. Следовательно, чтобы полностью определить эту группу, достаточно найти значение а 2= а * а. Этот элемент также должен принадлежать группе, поэтому у нас есть всего два варианта: либо а 2= е, либо а 2= а.

Последний вариант можно сразу же исключить из рассмотрения: применив закон сокращения к равенству а 2= а, получим, что а = е, но мы уже отмечали, что а и е отличаются. Следовательно, существует всего одна группа второго порядка.

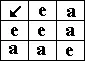
Группа второго порядка.

ЛЕВИ-СТРОСС: Я кое-что не понял: почему существует всего одна группа второго порядка? Ведь я могу заменить элемент а чем угодно.

ВЕЙЛЬ: Но таблица умножения не изменится. Важно не то, как выглядят элементы множества, а то, как они связаны между собой. Вспомните вашу историю с одуванчиком. Перестановки множества {1, 2, 3} не имеют ничего общего с преобразованиями, которые оставляют треугольник неизменным, но, как мы уже говорили, элементы обоих множеств можно объединить в пары так, что групповая операция будет корректной. С точки зрения структуры две эти группы будут неразличимы, изоморфны. Они подобны двум различным воплощениям одной и той же идеи

60

Платона — группы шестого порядка, отношения между элементами которой приведены в таблице. Понимаете?

ЛЕВИ-СТРОСС: Следовательно, существует всего одна «идея Платона» о группе третьего порядка?

ВЕЙЛЬ: Да, всего одна.

ЛЕВИ-СТРОСС: Дайте мне попробовать. Группа третьего порядка содержит е и два других элемента а и b, все ее элементы различны: G = {е, а, b}. Нам известно, что элементы группы связаны следующими отношениями: е * е = е, е*а = а*е = а и е*b = b*е = b. Попробуем вычислить значение а 2. Так как это элемент группы, допустимы всего три варианта: a 2= е, a 2= а и a 2= b. Тем не менее мы вновь можем исключить из рассмотрения а 2= а — в этом случае по закону сокращения элемент а будет равен нейтральному элементу. Остается два варианта: а 2= е и а 2= b. Но это означает, что существуют две разновидности групп третьего порядка!

ВЕЙЛЬ: Ваши рассуждения следует немного уточнить. Допустим, что а 2= е.

Тогда таблица, описывающая эту группу, будет начинаться так:

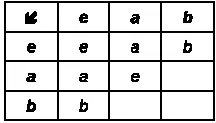
Мы уже доказали, что таблица умножения группы — это латинский квадрат, поэтому в каждом столбце и каждой строке таблицы должны быть записаны все элементы группы. Во второй строке уже записаны а и е, следовательно, в третьей ячейке этой строки может находиться только b, но тогда в третьем столбце b будет записано дважды. Эту таблицу нельзя дополнить так, чтобы в каждой строке и в каждом столбце были записаны все элементы группы. Следовательно, таблица не может описывать группу, и вариант a 2= е исключен.

ЛЕВИ-СТРОСС: Таким образом, остается всего один вариант: a 2= b. Очень интересно! Следовательно, мы можем записать группу так: G = {е, а, a 2}. Верно?

ВЕЙЛЬ: Осталось указать, каким будет результат операции над а и a 2, то есть каким будет значение a 3. Найти его очень просто: так как элемент a 3принадлежит группе, он может равняться только е, а или a 2. Тем не менее, если бы a 3был равен одному из двух последних элементов, то, применив закон сокращения один или два