Хавьер Фресан - Мир математики: m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

Предложение 1. Конечная абелева группа, порожденная двумя элементами, является либо циклической, либо прямым произведением двух циклических групп.

Это предложение — частный случай теоремы о структуре конечнопорожденных абелевых групп, по которой такие группы изоморфны прямому произведению

ℤ × ... × ℤ × ℤ/n 1× ... × ℤ/n k

где ℤ — группа целых чисел, a ℤ/n 1..., ℤ/n k— циклические группы. Число копий ℤ, приведенных в произведении, называется рангом группы и отлично от нуля тогда и только тогда, когда группа является бесконечной.

ЛЕВИ-СТРОСС: Теперь рассмотрим наш пример. В нотации, которую вы объяснили в прошлый раз, перестановки f и g записываются так:

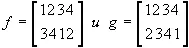
Переставим их двумя возможными способами:

Как видите, их композиция коммутативна, следовательно, в нашей структуре с обобщенным обменом любой мужчина может жениться на дочери брата своей матери.

ВЕЙЛЬ: Так как подгруппа S4, порожденная f и g, является абелевой, она будет либо циклической, либо прямым произведением двух циклических групп. В этом случае расчет

73

показывает, что перестановка f определяется как сочетание g с самой собой (/ =

= g2). Следовательно, мы имеем дело с первой из возможных ситуаций. Быть может, так будет всегда? Вовсе нет: составим пример, в котором подгруппа, порожденная f и g, будет прямым произведением двух циклических групп. Предположим, что допустимы следующие разновидности брака:

(Mt) мужчина А и женщина D

(M 2) мужчина В и женщина С

(M 3) мужчина С и женщина В

(M 4) мужчина D и женщина А

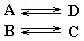
В этом случае кланы А и D, равно как и В и С, обменялись женщинами, следовательно, мы имеем дело с ограниченным обменом. Предположим, что дети матерей из кланов А, В, С и D принадлежат к кланам В, A, D и С соответственно. Мы можем определить функции f и g прежним образом:

Обратите внимание, что f — та же перестановка, что и в предыдущем примере, а перестановка g изменилась. Но и в этом случае их композиция коммутативна: 11

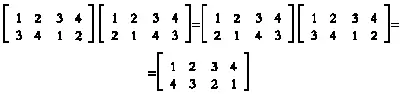
Отличие от предыдущего примера заключается в том, что теперь и f, и g являются элементами второго порядка (убедитесь в этом), следовательно, ни один из них не может быть степенью другого. Следовательно, подгруппа, порожденная f и g, будет произведением двух циклических групп. Более того, это будет группа Клейна!

ЛЕВИ-СТРОСС: Еще один вопрос, который интересует нас, этнологов, при изучении браков, звучит так: можно ли найти группы людей, которые не связаны

74

отношениями родства между собой? Общество, в котором можно выделить такие группы, называется сократимым. Допустим, что в элементарном племени, состоящем из четырех кланов, ограниченный обмен проводится по следующим правилам:

(Mt) мужчина А и женщина В

(M 2) мужчина В и женщина А

(M 3) мужчина С и женщина D

(M 4) мужчина D и женщина С

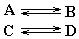
Дети принадлежат к тем же кланам, что и их матери. Функции f и g вычисляются как и обычно, однако будет не лишним напомнить, как именно это делается. В браке М 1жена принадлежит к клану В, следовательно, к этому же клану будут принадлежать и ее дети. Мужчина из клана В вступает в брак по правилу M 2, поэтому f(M 1) = M 2a g(M 1) = M 1так как женщины из клана В подчиняются первому правилу. Получим таблицу

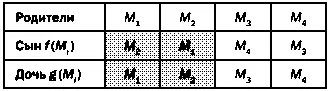
Очевидно, что кланы А и В никогда не породнятся с кланами С и D. Следовательно, рассматриваемое общество является сократимым. В противном случае общество называется несократимым.

ВЕЙЛЬ: Обратите внимание, господин Леви-Стросс, что достаточно рассмотреть несократимые общества, поскольку любое племя можно разделить на несколько несократимых сообществ. Это лишь одно из множества проявлений общего принципа, используемого в самых разных областях математики: если какой-либо объект можно разделить на несколько простых, при этом правила разделения известны, то для анализа всех возможных объектов достаточно изучить эти простые объекты. Представим несократимые общества на языке теории групп. Общество является несократимым тогда и только тогда, когда две любые разновидности брака связаны между собой перестановками f и g, то есть если одну из них можно получить из другой посредством этих перестановок. Не будем забывать, что f и g позволяют восстановить все генеалогическое древо! Очевидно, что это свойство в вашем примере не выполняется: применив f и g к М 1мы можем получить только М 1и М 2

Тем не менее два первых общества являются несократимыми. Напомним таблицу, которую мы привели в самом начале:

75

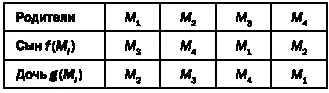
Докажем, что на основе брака Мх можно получить все остальные. В самом деле, применив f и g, получим M 3и M 2соответственно. Если же мы применим сначала f, а затем g, то получим M 4в силу равенства g(f(M 1)) = g(M 3) = M 4. Осталось показать, как можно получить М 1. Один из возможных вариантов — дважды применить f, так как f 2(M 1) = f(M 3) = М 1. Вот и все! Следовательно, рассматриваемое общество является несократимым.

ЛЕВИ-СТРОСС: Постойте, разве не нужно доказать это же утверждение, взяв за основу M 2, М 3и M 4вместо М 1?

ВЕЙЛЬ: На самом деле этого не требуется, и сейчас я объясню, почему. Мы знаем, что из Мх можно вывести все возможные разновидности брака. Допустим, что мы хотим вывести все разновидности брака из какого-либо другого M i. Обозначим через h элемент подгруппы, порожденной f и g, который позволяет перейти от М 1к M i, то есть такой элемент, для которого выполняется условие h(M 1) = M i.

Так как h принадлежит группе, для него определен обратный элемент h -1. Припишем h -1с двух сторон равенства и получим h -1(h(M 1)) = h -1(M i). Композицией h и h -1является тождественное преобразование — вспомните определение обратного элемента! Таким образом, Мх = h -1(M i). Это означает, что мы можем получить М 1из M i. Так как правило M 1связано со всеми остальными разновидностями брака, с ними будет связано и любое другое M i. Подгруппы S n, обладающие этим свойством, называются транзитивными. Имеем: