Хавьер Фресан - Мир математики: m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

Для двух положительных чисел а и b логарифмом а по основанию b (обозначается log b(a)) называется степень, в которую нужно возвести b, чтобы получить а.

Иными словами, с — логарифм а по основанию b, если числа а, b и с удовлетворяют соотношению b c= а. К примеру, известно, что log 2(4) = 2, log 2(8) = 3, так как 2 2= 4, а 2 3= 8. Вычислить логарифмы не всегда так легко. Нужно понимать, что логарифм преобразует частное в разность:

log b(x/y) = log b(x) - log b(y)

Продолжим рассматривать наш пример. Если основание логарифма равно b = 2, х = 8 и у = 4, то их частное равнялось бы 2, следовательно, левая часть выражения была бы равна log 2(2) = 1. С другой стороны, мы уже знаем, что log 2(8) = 3, log 2(4) = 2.

В этом случае формула вновь оказывается верной, так как 1 = 3 — 2. Эту формулу можно доказать в общем виде, применив основные свойства степеней. Попробуйте сами!

Мы знаем, что отношения частот последовательных нот совпадают, следовательно, логарифмы этих отношений также будут равны:

117

log b(f 2/f 1) = log b(f 3/f 4) = ... = log b(f 13/f 12)

С учетом приведенной выше формулы получим

log b(f 2) - log b(f 1) = log b(f 3) - log b(f 2) = ... = log b(f 13) - log b(f 12)

Это соотношение выполняется для любого положительного b. Выберем особое значение d, равное корню 12-й степени из 2, которое удовлетворяет уравнению d 12= 2

Совсем недавно я объяснил, что любое отношение частот последовательных нот равно d, поэтому если мы рассмотрим логарифмы по основанию d, то получим:

log d(f 2/f 1) = log d(f 3/f 4) = ... = log d(f 13/f 12) = log d(d) = 1

так как показатель степени, в которую нужно возвести d, чтобы получить d, равен единице. Таким образом, мы можем преобразовать логарифм частного в разность логарифмов и получить следующее равенство:

log d(f 2) - log d(f 1) = log d(f 3) - log d(f 2) = ... = log d(f 13) - log d(f 12) = 1

ЛЕВИ-СТРОСС: Что это означает? Я запутался!

ВЕЙЛЬ: Ах да, я и забыл, что это вы попросили у меня объяснений... Эти вычисления иллюстрируют следующую мысль: если мы рассмотрим не частоты f 1, f 2..., а их логарифмы по основанию d, то есть log d(f 1), log d(f 2), то для перехода от любой ноты к следующей достаточно будет прибавить единицу. А это полутон!

ЛЕВИ-СТРОСС: Мы до сих пор не обратили внимания на один очень важный момент. Взглянув на додекафонический круг, читатель может представить, что все ноты используются одинаково, но очевидно, что основную роль играет подмножество нот до, ре, ми, фа, соль, ля и си, которым соответствуют белые клавиши.

Обратите внимание, что эта последовательность составлена очень странным образом: чтобы перейти от до к ре и от ре к ми, нужно добавить тон, а чтобы перейти от ми к фа — только полутон, при этом ни на клавиатуре пианино, ни на круге это никак не обозначено. Далее мы последовательно добавляем тон, чтобы перейти от фа к соль, от соль к ля и от ля к си, но интервал между си и до вновь нарушит симметрию:

118

до →1→ ре →1→ ми →1/2→ фа →1→ соль →1→ ля →1→ си →1/2→ до.

Это тональность до мажор. Мы можем построить новые эквивалентные тональности, начиная с любой ноты — для этого нужно воспроизвести последовательность интервалов 1, 1, 1/2, 1, 1, 1, 1/2. В общем случае потребуется вносить альтерации.

Вспомните «Струнный квартет № 3» Шостаковича: рядом с названием указано «фа мажор».

Это в некотором роде означает, что доминантная нота в партитуре — не до, а фа, следовательно, будет уместно перестроить строй, начав с фа. Мы хотим, чтобы закономерность 1, 1, 1/2, 1, 1, 1, 1/2 сохранялась: фа и соль, соль и ля разделены одним тоном, но ля и си отстоят друг от друга не на полутон, как нам бы хотелось, а на целый тон, поэтому вместо си нужно рассмотреть ноту на полтона ниже, то есть си-бемоль. Продолжим: си и до, до и ре, ре и ми разделены целыми тонами, и наконец, интервал между ми и фа равен одному полутону, как мы и хотели.

Следовательно, тональность фа мажор получается заменой си на си-бемоль. Это обычно указывается рядом с ключом нотного стана, чтобы каждый раз не записывать альтерацию рядом с нотой си.

Тональность фа мажор.

В этом случае потребовалось добавить всего одну альтерацию, но посмотрите, сколько потребуется добавить, если мы начнем строй с фа-диез, как в удивительной неоконченной «Десятой симфонии» Малера. Фа-диез и соль разделены полутоном, а мы хотим, чтобы их разделял целый тон, поэтому заменим соль на соль-диез. Теперь соль-диез и ля разделены всего лишь полутоном, следовательно, ля также нужно заменить на ля-диез. Ля-диез и си разделены полутоном, как и полагается, однако интервал между си и до также равен полутону, но нам нужен целый тон, поэтому заменим до на до-диез. В результате расстояние до ре уменьшится до полутона, следовательно, необходима альтерация ре и ми. Наконец, ми-диез отделяет от фадиез один полутон (как вы помните, ми-диез и фа — одна и та же нота), как мы и хотели. Следовательно, чтобы составить строй фа-диез мажор, нам пришлось альтерировать шесть из семи нот!

119

фа# соль# ля# си до# ре# ми# фа#

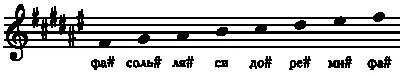
Тональность фа-диез мажор.

ВЕЙЛЬ: Из вашего объяснения, господин Леви-Стросс, становится понятно, что транспонирование на одну кварту (пять полутонов) едва заметно, так как изменяется всего одна нота стандартного строя. Когда мы хотим выполнить плавную транспозицию между двумя тональностями, удобнее выполнить переход через несколько промежуточных кварт. Такой переход возможен всегда, поскольку [5] порождает «группу часов»; иными словами, все элементы этой группы можно получить повторным сложением [5] с самим собой. К примеру, транспонирование на малую терцию (три полутона) эквивалентно транспонированию на три кварты, так как

[5] + [5] + [5] = [3].

С тритоном (интервалом в шесть полутонов) все происходит с точностью до наоборот. Если мы применим эту транспозицию два раза, то ничего не изменится, так как [6] + [6] = [0]. Вы наверняка слышали о дьяволе в музыке. В Средневековье церковь запрещала использовать тритон, так как данный аккорд отличался резким, неустойчивым звучанием и поэтому мог быть только творением дьявола. Тритон естественным образом возникает в аккорде ноты си. Как вы наверняка помните, классические аккорды исполняются на белых клавишах пианино «через одну»: к примеру, ДО ре МИ фа СОЛЬ — аккорд до, а СОЛЬ ля СИ до РЕ — аккорд соль. Обратите внимание, что в обоих случаях крайние ноты аккордов разделены семью полутонами. Этим свойством обладают все аккорды за исключением тех, что начинаются с ноты си, так как общая длина аккорда СИ до РЕ ми ФА составляет шесть полутонов — проклятый тритон. Вот он, дьявол в музыке! Лишь в эпоху барокко запреты ослабли, и тритон вновь начал использоваться в музыкальных произведениях при переходе в другие тональности и для почеркивания важных элементов композиции.