Хавьер Фресан - Мир математики: m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

ЛЕВИ-СТРОСС: Все изменилось с началом романтизма. Одна из первых композиций, где в полной мере проявляется дьявол в музыке, — это «Соната по прочтении Данте» Ференца Листа. Первая тема сонаты написана в ре минор.

Пока что я говорил только о мажорных тональностях в музыке; сейчас я вкратце объясню, что означает «минор». Вновь рассмотрим строй до, ре, ми, фа, соль, ля, си.

Представим его в виде круга. Сразу же возникает вопрос: что произойдет, если мы «повернем» ноты?

120

Получим, к примеру, строй ля, си, до, ре, ми, фа, соль, в котором уже не будет соблюдаться последовательность интервалов 1,1,1/2,1,1,1,1/2, следовательно, этот строй не будет эквивалентен исходному. Следовательно, будет интересно посмотреть, что произойдет, когда полутона будут располагаться иначе.

В нашем примере полутона расположены во второй и пятой позиции: 1, 1/2, 1, 1, 1/2,1,1. Звукоряды, которые описываются этой последовательностью, называются минорами. Так, строй ля минор соответствует строю до мажор. В общем случае, чтобы определить соответствующий минор, нужно отсчитать три полутона вниз, начиная с первой ноты. Так, тональности ре минор соответствует фа мажор.

Соответствие между минорами и мажорами.

Крайне важно отметить, что альтерации соответствующих миноров и мажоров совпадают, следовательно, для того чтобы определить, в минорной или мажорной тональности написано произведение, одних лишь альтераций недостаточно. Необходимо использовать другие, более субъективные критерии, например определить, какой нотой чаще всего заканчиваются звуковые последовательности в мелодии.

ВЕЙЛЬ: Ваше объяснение тональностей, господин Леви-Стросс, вновь наводит на подозрения, что не все ноты додекафонического круга играют одинаково важную роль в мелодии. Это казалось Арнольду Шёнбергу невыносимым, поэтому пока Эйнштейн уточнял детали своей первой теории относительности, Шёнберг написал «Камерную симфонию», с которой начался закат тональной музыки. Новое направление достигло вершины в 20-е годы XX века, когда создатель додекафонии начал претворять в жизнь программу об абсолютном равенстве всех 12 нот в любой композиции. Эта программа нашла яркое воплощение в работах композиторов Нововенской школы.

121

ЛЕВИ-СТРОСС: Я помню, как впервые прикоснулся к этой новой музыке.

С малых лет родители по воскресеньям водили меня в оперу Гарнье и другие концертные залы. Не забывайте, моим прадедом по материнской линии был скрипач Исаак Стросс (Штраусс), который работал с Оффенбахом и был знаком с Россини.

Дух прадеда сохранился в нашей семье, но история моего знакомства с музыкой окончилась произведениями Вагнера. Я открыл для себя Шёнберга, Альбана Берга, Антона Веберна и испытал подлинную страсть к звукам, которые услышал в первый раз. Кажется, я так и не смог привыкнуть к их творчеству. Не говоря уже о сериалистах, например о Лучано Берио, которые выступают за равноправие не только частот звуков, но и их длительности, тембра и любых других измеримых параметров.

Это направление разочаровало меня и совершенно сбило с толку, поскольку некоторые голоса «Симфонии» выкрикивали тексты из моей книги «Сырое и приготовленное». Но я допускаю, что перестать быть человеком XIX века не так-то просто.

ВЕЙЛЬ: Я не удивлен, что эта музыка показалась вам принципиально новой, так как многие шедевры додекафонической музыки написаны на основе латинского квадрата. Вы уже знаете, что латинский квадрат — всего лишь таблица, в которой определенное множество символов (в нашем случае — 12 нот) записано так, что в каждой строке и в каждом столбце содержатся все символы множества. На первом шаге выбирается последовательность, состоящая из 12 нот, на основе которой по установленным правилам строится латинский квадрат. Следовательно, существует столько же «руководств по музыкальной композиции», сколько и упорядоченных последовательностей нот до, до-диез, ре, ре-диез, ми, фа, фа-диез, соль, соль-диез, ля, ля-диез и си, всего 479001600 последовательностей.

ЛЕВИ-СТРОСС: Это меньше, чем «Сто тысяч миллиардов стихотворений» Кено.

ВЕЙЛЬ: Однако это число достаточно велико, чтобы композиторы могли попрежнему испытывать иллюзию свободы творчества, не правда ли? Как я уже говорил, суть метода заключается в том, чтобы упорядочить 12 нот, например следующим образом:

ми — соль — фа-диез — ля — соль-диез — до — фа — ре — ре-диез —

— до-диез — си — ля-диез.

В ключе соль эта последовательность записывается так:

122

ми соль фа-диез ля соль-диез до фа ре ре-диез до-диез си ля-диез

а в ключе фа — следующим образом:

ми соль фа-диез ля соль-диез до фа ре ре-диез до-диез си ля-диез

Следовательно, первая строка таблицы будет выглядеть так:

ми | соль | фа-диез | ля | соль-диез | до | фа | ре | ре-диез | до-диез | си | ля-диез

Первую строку таблицы можно записать и по-другому, определив место каждой ноты в «группе часов». При выполнении операций, позволяющих построить весь латинский квадрат на основе первой строки, крайне полезно сопоставить «полдень» «группы часов» первой выбранной нами ноте, то есть сделать ноту ми нейтральным элементом группы.

Следовательно, повернем «часы» так, чтобы нота ми заняла положение, которое обычно занимает нота до, после чего скопируем числа последовательности.

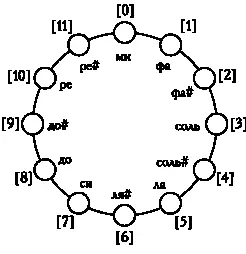
123

Напомню, что мы записали числа в квадратных скобках, чтобы указать: [3] обозначает не только число 3, но и все числа, которые можно получить, прибавив или отняв 12: 3, 15, 27,—9,—21. Таким образом, первую строку нашего латинского квадрата можно записать в следующем виде:

[0] | [3] | [2] | [5] | [4] | [8] | [1] | [10] | [11] | [9] | [7] | [6]

ЛЕВИ-СТРОСС: Понятно. Каким будет второй шаг?

ВЕЙЛЬ: После того как мы получили основную последовательность, заполним первый столбец таблицы, применив инверсию. Любые две ноты первой строки разделены некоторым интервалом. Инверсия заключается в том, чтобы воспроизвести те же самые интервалы в противоположном направлении. К примеру, ми и соль разделены тремя восходящими полутонами (ми — фа — фа-диез — соль), следовательно, инверсия этого интервала заключается в том, чтобы отсчитать три полутона вниз: ми — ре-диез — ре — до-диез. Получается, во второй клетке первого столбца запишем: до-диез. Другой пример: соль и фа-диез разделены восходящим полутоном, следовательно, нужно подняться на один полутон от ноты до-диез, которую мы только что получили. В результате имеем ноту ре. Выполнив аналогичные действия, получим первый столбец: