Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— И я! — отозвалась Вертикальная Стрелка.

— Понятно? — спросил Мнимий Радиксович.

Илюша поглядел на стрелки и не совсем уверенно сказал:

— Маленькие стрелки на осях — ведь это его проекции?

Мнимая ось.

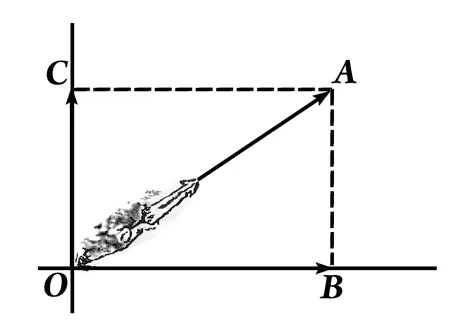
Действительная ось.

Стрелка ОА есть геометрическая сумма стрелок ОВ и ОС , которая получается по правилу сложения сил в механике. Стрелка ОА есть ( a+ bi ); стрелка ОВ есть а ; стрелка ОС есть bi .

— Точно! — ответил Радикс.

— А кроме того, это похоже на параллелограмм сил. Выходит, что Наклонная Стрелка есть сумма тех стрелок, которые на осях?

— Или?.. — важно спросил Мнимий.

Илюша молчал.

— Если, — сказал Мнимий, — Наклонная Стрелка является геометрической суммой осевых стрелок, то, следовательно, эти стрелки по отношению к Наклонной Стрелке суть…

— 398 —

— …ее слагаемые, — отвечал Илюша. — Пожалуй, лучше сказать: ее составляющие.

— Вот это да! — отвечал Мнимий. — Так и запишем. Итак, каждый комплексный человечек может быть рассматриваем как сумма вещественной составляющей и мнимой, что нам давно известно из формулы:

a+ bi

А теперь вы видите, как это можно изобразить геометрически.

Далее мы попросим нашего друга комплексного Вектора уменьшиться так, чтобы он был ростом в одну единицу.

Вектор-Наклонная-Стрелка немедленно сделался покороче.

— Как раз! — сказал Мнимий. — Ровно единица!

Осевые стрелки тоже сделались соответственно короче.

— Ну-с, — сказал Мнимий Илюше, — вы ничего не замечаете?

— Не знаю, — отвечал Илюша.

Тогда Вектор-Наклонная-Стрелка быстро повернулся против часовой стрелки, и кончик его туфелек начертил круг.

— А теперь? — спросил Мнимий.

Картина перед Илюшей несколько изменилась. Линии осей, уходившие за черту круга, исчезли. Все линии стали очень тоненькими, исключая проекцию Вектора-Наклонной-Стрелки на действительную ось и того перпендикуляра, который опускался от конца Вектора на конец этой проекции. Эти линии, наоборот, стали очень толстыми и черными.

— Не узнаете? — спросил Мнимий.

— Узнаю как будто, — сказал Илюша. — Это синус и косинус.

— Ага! — вскричал Мнимий. — Они самые. Ну-ка, прикиньте, что бы это могло значить алгебраически? Как выходит, что проекции единичного вектора суть синус и косинус?

— Потому, вероятно, — отвечал Илюша, — что синус в квадрате и косинус в квадрате, как катеты прямоугольного треугольника, равны гипотенузе в квадрате, а она у нас равна единице. Радиус ведь и есть единица. Вектор в данном случае и есть радиус.

— Ну что ж, — отвечал Мнимий, — вы правы. Но давайте разберемся в этом. Если нам дан на комплексной плоскости, которую вы видите сейчас перед собой, некий комплексный вектор, то ответьте, чем он, по-вашему, отличается от обыкновенных чисел?

— Он как сила в механике, — ответил Илюша, — имеет направление.

— 399 —

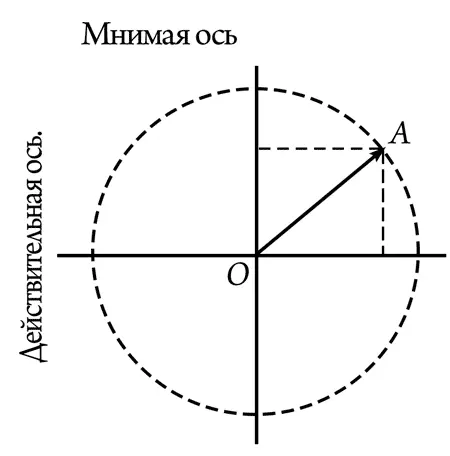
— Мне очень нравится ваш ответ, — вежливо отвечал Мнимий, — но давайте посмотрим еще на наш чертеж и разберем все подробней. Итак, значит, длину вектора мы…

— … определяем по теореме Пифагора, — подхватил Илюша.

— Любого вектора?

— Любого.

— Напишите! — сказал Мнимий.

Илюша написал:

r = √( a 2+ b 2).

Что это за линии OB и BA ?

Кто скажет?

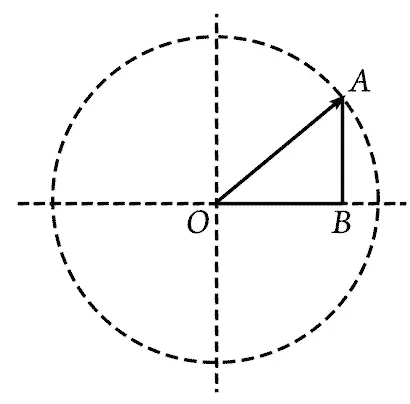
— Отменно! — произнес Мним. — Далее, если вектор наклонен по отношению к положительному направлению вещественной оси под углом φ , то как бы вы определили проекции вектора на оси, исходя из длины его и данного угла?

— По-моему, надо вот как написать:

а = r cos φ ;

b = r sin φ .

— Справедливо! А что если нам теперь взять наш вектор в обычной форме:

a + bi

и подставить в его выражение новые значения для а и b ?

а + bi = rcos φ + ( rsin φ ) i = r(cos φ + i sin φ ).

— Теперь, — заявил Мнимий, — получилась так называемая тригонометрическая форма комплексного числа.

Ясно, что множитель перед скобкой есть длина вектора, или его модуль. А что же стоит в скобках?

— 400 —

Угол с положительным направлением вещественной оси определяет направление вектора.

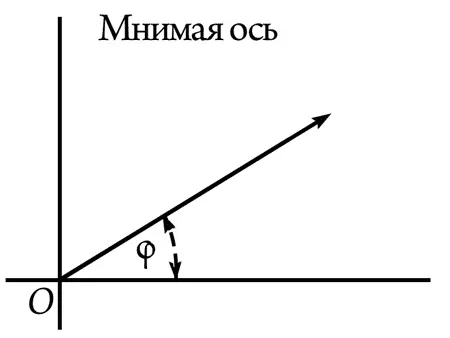
— Мне кажется, что это тоже вектор.

— Справедливо. А длина его?

— Равна единице.

— Точно. Потому он и называется единичным вектором.

А величина, определяющая направление вектора, именуется его аргументом. Очевидно, любой вектор можно изобразить, выбрав соответствующий аргумент и приличный случаю модуль.

— Ясно, — отвечал Илюша. — Умножил на сколько надо и получил из единичного вектора такой, какой требуется.

— Точно, правильно, прекрасно! — произнес Радикс.

— В таком случае давайте рассмотрим, что будет с единичным вектором, если его умножить на самого себя:

(cos φ + isin φ ) (cos φ + isin φ ) = (cos 2 φ— sin 2 φ ) + 2 isin φ · cos φ .

— Ну, Илюша, — сказал Радикс, — глянь-ка повнимательней: тебе эта формула ничего не говорит?

Илюша пожал плечами.

— Тогда вот что, — сказал Мнимий Радиксович. — Может быть, в дальнейшем вы заглянете в учебник тригонометрии и узнаете, что разность квадратов косинуса и синуса есть косинус двойного угла φ , то есть угла, равного двум φ . А удвоенное произведение косинуса φ на синус φ есть аналогично синус угла двух φ . Если записать, то выйдет:

cos 2 φ = cos 2 φ — sin 2 φ

sin 2 φ = 2 sin φ · cos φ .

Минуя некоторые длинные выкладки, сделаем такое общее заключение: возвести единичный вектор в степень n значит увеличить его угол в n раз. Вот что означает геометрически возведение единичного вектора в степень.

— Как будто, — сказал очень нерешительно Илюша, — я это где-то даже видел.