Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— 283 —

страшный грохот, целое облако дыма вырвалось из широкого дула пистоли, по, несмотря на все эти пиротехнические эффекты, пуля летела так медленно, что Илюша видел, как она мелькнула по внутренней стороне полусферы, оставив за собой тонкий след в виде царапины по стеклу.

— Попал! — крикнул Коникос. — Какая меткость! С первого раза!

Илюша удостоверился, что пуля, обогнув полусферу, прошла как раз над вершиной треугольника ( В ) и ушла в пол.

Затем Коникос снова зарядил пистолю, подсыпал пороху на полку, стал опять на то же место, но повернулся теперь лицом в сторону другого угла ( А ), который был с правой стороны основания треугольника. Снова бах! Пуля прошла как раз над вершиной справа у основания.

Затем Коникос перешел в тот самый угол, над вершиной которого только что прошла пуля. Теперь он стал в этот правый угол ( А ) и лицом обратился снова к углу в вершине ( В ).

Снова он поднял пистолю над головой, так что она стояла почти вертикально, то есть почти перпендикулярно к полу, а затем опять трах! Снова целое извержение порохового дыма, и опять мелькнула пуля, царапая стекло.

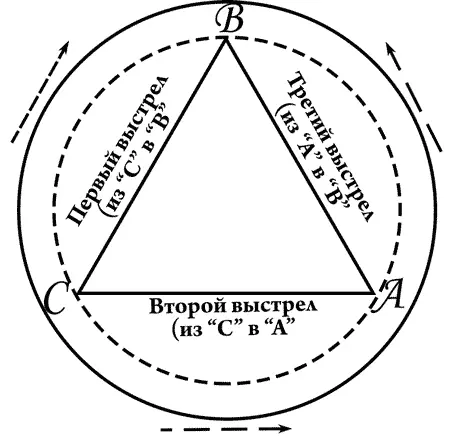
Вот такой треугольник начертил на полу Коникос, стоя под полусферой.

— Вот выстрел! Поищи-ка, где пересекаются оба следа.

Илюша обошел сферу, подошел к углу при вершине и убедился, что оба следа пересеклись в точке, лежащей как раз над вершиной В треугольника.

Затем Коникос выполз из-под полусферы и сказал:

— Я полагаю, что пули летели «совершенно прямо», в неевклидовом смысле слова, как это им и свойственно. Они бы, разумеется, летели иначе, если бы им стекло не мешало и они не были бы обязаны сохранять вертикальную плоскость полета, но тут уж им при всей их любви к прямолинейности и краткопутности ничего другого не оставалось! Теперь я попрошу полусферу уменьшиться до полуметра в диаметре, дабы мы имели возможность обозреть результаты моей неподражаемой стрельбы в цель.

— 284 —

Полусфера сейчас же послушалась, и Илюша увидел, что пули начертили на стекле своеобразный треугольник. Тогда Асимптотос взял свой широченный нож и сказал мальчику:

Срез полусферы (экватор)

— Смотри: плоскость моего ножа, то есть секущая плоскость, стоит сейчас перпендикулярно к той плоскости, на которой лежит половина сферы. Ясно?

— Ясно.

— Я сделаю три сечения. Каждый раз нож будет стоять перпендикулярно к плоскости, на которой лежит полушар.

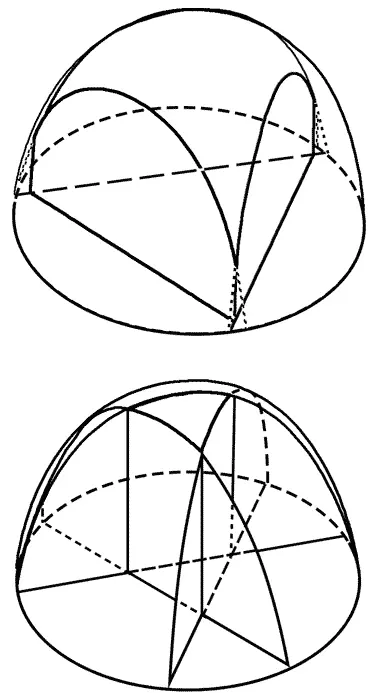
Затем Асимптотос аккуратно провел разрез так, что линия его шла от точки А к точке В . Второй разрез соединил точки В и С, а третий — точки С и А . И все разрезы шли в точности по царапинам, оставленным пулями. Затем он вынул из середины сферы получившийся кусок и дал его Илюше.

— Заметь, — сказал Асимптотос, — что если вершины треугольника будут лежать на самом срезе полусферы, то есть на ее экваторе, то все дуги «прямых», то есть вертикальных сечений сферы, проходящие через эту точку, будут иметь общую касательную вертикаль, а угол, образованный этими дугами, поэтому будет

— 285 —

равен нулю. (Вспомни, как Коникос учил тебя измерять угол между кривыми!) Но если немного сдвинуть вершину треугольника вверх по полусфере, как мы это сделали, то касательные наклонятся и разойдутся: это и даст нам возможность применять нашу пистолю. Но так как мы сдвинулись немного вверх, то и угол между двумя положениями ствола пистоли Коникоса, то есть угол треугольника, будет очень мал, и он будет тем меньше, чем ближе вершина к экватору. Я вырежу еще такой же треугольник, только расположенный повыше и площадью поменьше.

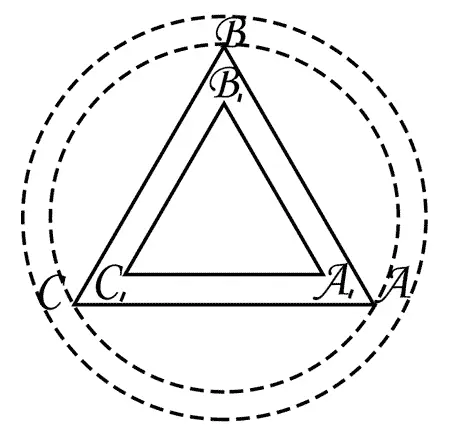
Снова Асимптотос начертил круг, затем снова вписал в него равносторонний треугольник ABC , а затем начертил внутри этого треугольника еще один — А 1 В 1 С 1, поменьше, подобный первому и симметрично расположенный. (Смотри на картинке, стр. 284 {11} 11 Ошибка. В печатном оригинале этот чертеж расположен на странице 285. В электронном варианте чертеж перенесен в соответствии со ссылкой — V_E. .)

После этого он взял нож и вырезал еще один треугольник, уложив, разумеется, предварительно на чертеж еще одну половину сферы.

— А теперь, — заявил Коникос, — мы будем утверждать, что данные два треугольника по своим свойствам суть не что иное, как треугольники Лобачевского! Доказать тебе, наш юный друг, это обстоятельство было бы хлопотливо, однако это так. Поверь на слово. Был один француз-математик в истекшем столетии, который нашел это и доказал довольно-таки точно и неоспоримо.

Нахмуренная физиономия доктора У. У. Уникурсальяна немедленно появилась среди почтенной компании.

— Не следует, — сказал он, — утверждать того, чего ты не можешь доказать.

— Докажи, что я неправ! — предложил Коникос.

Но в ответ на это Доктор Четных и Нечетных почему-то отвернулся да и растаял втихомолку.

— Теперь далее! — наставительно произнес Асимптотос. — Слушай-ка хорошенько да мотай на ус. Тебе, я думаю, совершенно ясно, что эти два плоскостных треугольника, которые у меня были чем-то вроде выкроек для не-евклидовых треугольников, подобны друг другу?

— Абсолютно ясно! — заявил Илюша.

— А ну-ка, — продолжал словоохотливый старичок, — проверим-ка, подобны ли эти два удивительных не-евклидовых треугольника.

Сперва Илюша не мог сообразить, как ему взяться за эту проверку подобия, но затем придумал. Он положил оба треугольника на половинку сферы. Большой треугольник кое-как закрепил (кажется, кнопками), а малый стал передвигать так, что он скользил по сфере и по большому треугольнику. Он

— 286 —

рассуждал: если эти треугольники подобны, то углы у них равны, а следовательно, можно вдвинуть один из углов малого треугольника в один из углов большого, а если углы равны, то две стороны малого должны совпасть с двумя сторонами большого. Сказано — сделано! И вот, представьте себе, когда он пододвинул один из углов малого треугольника к одному из углов большого, то стороны малого не только не пошли по сторонам большого, не только не совпали с ними, а даже закрыли стороны большого, так что Илюша должен был заключить, что углы малого треугольника больше — и заметно больше! — углов большого треугольника.