Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

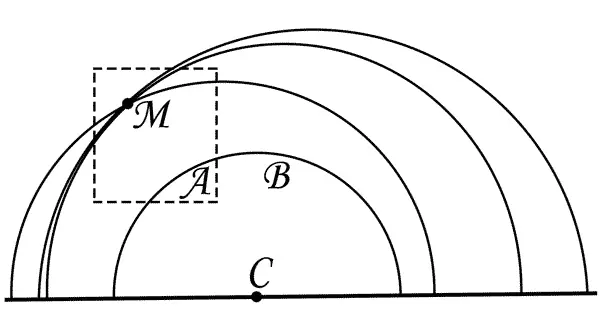
Через точку М проведено несколько «прямых», не пересекающих «прямую» АВ .

— 293 —

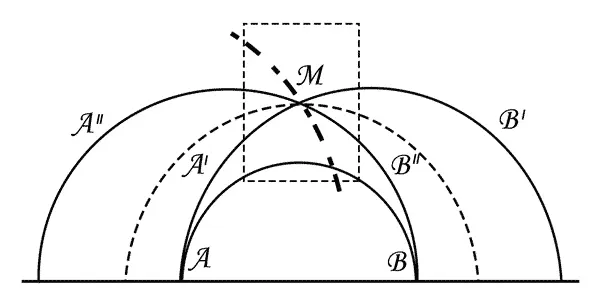
«Прямая» А ′ В ′параллельна АВ , в сторону А ; «прямая» А ′′ В ′′параллельна АВ в сторону В . «Прямые», проходящие внутри углов А ′ МА ′′и В ′ МВ ′′,«расходятся» с АВ . «Прямые», проходящие внутри углов А ′ МВ ′′и В ′ МА ′′,пересекают АВ .

— Потому что они похожи на евклидовы и в них сумма углов почти равна ста восьмидесяти градусам! — воскликнул Илюша. — Кажется, я начинаю наконец разбираться понемногу…

Тут Илюша снова откуда-то услыхал звуки флейты Фавна.

Обернувшись, он увидел, что его хитрая рожица выглядывает из-за уголка цветной занавеси домика. Он протягивал Илюше правую руку и манил его к себе левой.

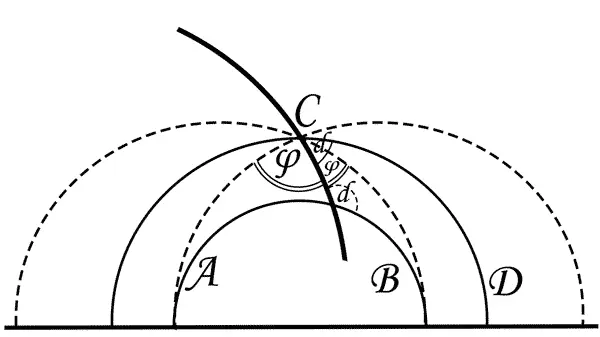
Два перпендикуляра — АВ и CD — к одной «прямой» «расходятся» — угол параллельности φ острый

— 294 —

— Ты только попробуй! — произнес Фавн шепотом. — Никогда никто не кушал ничего вкуснее!

— Может быть, это и стыдно, — сказал Илюша, отломив втихомолку добрый кусочек казанского сыра и делая вид, что он никакого Фавна и в глаза не видел, — но я должен сознаться, что я тоже до сих пор думал, что геометрия Евклида единственная.

— Стыдного тут ничего нет, — отвечал Асимптотос. — Ты просто не знал, вот и все. Но спорить с построенной системой — это уже совсем другое дело.

— Значит, я уже узнал здесь, кроме евклидовой, три новые геометрии: геометрию лабиринтов, потом геометрию Лобачевского и геометрию Птолемея…

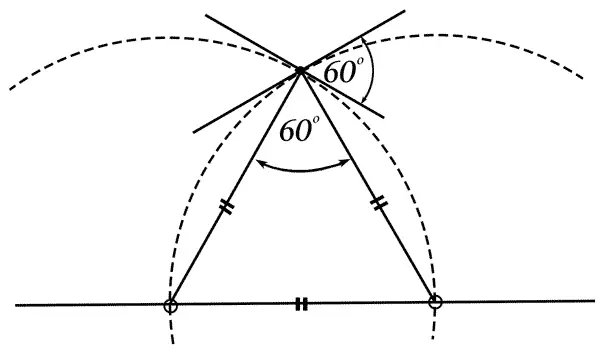
Угол между двумя окружностями одного радиуса, из которых каждая проходит через центр другой, равен 60 градусам.

— То есть сферическую, — заметил Копикос. — Однако я могу тебе показать еще одну геометрию. Это будет геометрия теней. Ты увидишь сейчас удивительные тени. Слышал ли ты такой стишок:

Неужели ты его не знаешь? Почитай, голубчик! Его написал прекрасный русский поэт Александр Блок. Это почти эти самые тени и есть.

— 295 —

В треугольнике ABC углы А и В близки к 60 градусам, а угол С очень мал, поэтому сумма углов этого треугольника немногим больше 120 градусов.

Асимптотос притащил откуда-то лампочку очень странной и красивой формы, немножко похожую на чайник, в носик которого был вставлен фитиль. Лампа горела не очень ярко, но все-таки светила. В ней было налито нечто вроде оливкового масла. Говорят, будто это была та самая лампа, из-за которой начались несчастья бедной Душеньки в той самой поэме Богдановича, которую так любил юный Пушкин, потому что Aпyлей (сочинивший книгу «Золотой осел», где изложена история Душеньки) ему нравился гораздо больше рассудительного Цицерона [20] О том, как Пушкин в юности Читал охотно Апулея, а Цицерона не читал, ты можешь узнать из «Евгения Онегина». А поэма Богдановича так и называется «Душенька». . Масло для этой лампы Коникос зачерпнул из фонтана. Затем Коникос сделал какой-то странный жест, и в светлице стемнело. Только и было света, что от масляной лампы.

Асимптотос поставил ее на стол и вырезал круглый кусочек плоскости.

— Смотри теперь на тень этого кружка. Если я поставлю мой диск вертикально параллельно стене на одном уровне с источником света, то и тень на стене получится…

— Круглая, — отвечал Илюша.

— Справедливо. Теперь смотри, что будет с тенью, если я буду поворачивать кружок вокруг его вертикального диаметра. Если я поверну кружок на некоторый угол так, чтобы диск у меня стоял наклонно к плоскости стены, то тень будет…

— 296 —

— Эллипсом! -отвечал Илюша.

— А теперь, — продолжал Коникос, — смотри, какие тени будут получаться от кружка на столе. Если я опущу диск ниже пламени, то на столе получится… На-ка, возьми диск, попробуй сам!

Илюша взял диск, опустил его немного ниже пламени лампы и получил две тени: эллиптическую и круговую, которые он уже видел на стене.

— Теперь, — сказал Асимптотос, — слушай мою команду! Поставь диск вертикально так, чтобы самая высокая его точка находилась на уровне пламени.

Илюша поставил. Тень от кружка стала с одной стороны овальной, а с другой — уходила прямо по столу, и казалось, что две стороны тени уходят вдаль, стремясь сделаться все более и более параллельными.

— Эта тень похожа, — сказал Илюша, — пожалуй, опять на кривую квадратного уравнения.

— Справедливо, — отвечал Коникос. — Ты получил параболу. А теперь подними кружок еще немного повыше, так, чтобы его горизонтальный диаметр был на уровне пламени.

Илюша приподнял кружок. Теперь на стол падала тень только от нижней части кружка. С одной стороны она тоже была похожа на овал, но с другой стороны тень уходила до самого края стола. Однако ее стороны не стремились к параллельности, а шли почти прямо в разные стороны.

— А это что такое?

— Н-не знаю, — сказал Илюша. — Но так как мы видели все конические сечения, кроме гиперболы, это, наверное, она и есть?

— Она самая. А скажи, пожалуйста, не встречал ли ты гиперболу вечером на улице?

— На улице? — удивился Илюша. — Нет, кажется, не встречал.

— А видал ли ты вечером на улице такую картину: у подъезда дома стоит автомобиль с одной зажженной фарой, и свет от фары падает на мостовую?

— 297 —

—Это я, конечно, видал, — ответил Илюша.

— Так вот имей в виду, что освещенный кусок мостовой и рисует на асфальте самую настоящую гиперболу, то есть одну из ее ветвей. Почему? Потому что световой пучок выходит из фары конусом, а мостовая в данном случае является секущей плоскостью по отношению к этому конусу. Когда увидишь эту гиперболу в следующий раз, кланяйся ей от меня… Эта геометрия теней называется проективной геометрией. Вот тебе и пятая геометрия! Учи только, не ленись, у нас геометрий хватит!